
Too Much Data: Prices and Inefficiencies in Data Markets
∗
Daron Acemoglu
†
Ali Makhdoumi
‡
Azarakhsh Malekian
§
Asu Ozdaglar
¶
Abstract
When a user shares her data with an online platform, she typically reveals relevant information
about other users. We model a data market in the presence of this type of externality in a setup
where one or multiple platforms estimate a user’s type with data they acquire from all users and
(some) users value their privacy. We demonstrate that the data externalities depress the price of
data because once a user’s information is leaked by others, she has less reason to protect her data
and privacy. These depressed prices lead to excessive data sharing. We characterize conditions
under which shutting down data markets improves (utilitarian) welfare. Competition between
platforms does not redress the problem of excessively low price for data and too much data shar-
ing, and may further reduce welfare. We propose a scheme based on mediated data-sharing that
improves efficiency.
Keywords: data, informational externalities, online markets, privacy.
JEL Classification: D62, L86, D83.
∗
We are grateful to Alessandro Bonatti and Hal Varian for useful conversations and comments. We gratefully ac-
knowledge financial support from Google, Microsoft, the National Science Foundation, and the Toulouse Network on
Information Technology.
†
Department of Economics, Massachusetts Institute of Technology, Cambridge, MA, 02139 . [email protected]
‡
Fuqua School of Business, Duke University, Durham, NC, 27708 [email protected]
§
¶
Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge,
MA, 02139 [email protected]

1 Introduction
The data of billions of individuals are currently being utilized for personalized advertising or
other online services.
1
The use and transaction of individual data are set to grow exponentially
in the coming years with more extensive data collection from new online apps and integrated
technologies such as the Internet of Things and with the more widespread applications of artificial
intelligence (AI) and machine learning techniques. Most economic analyses emphasize benefits
from the use and sharing of data because this permits better customization, better information,
and more input into AI applications. It is often claimed that because data enable a better allocation
of resources and more or higher quality innovation, the market mechanism generates too little data
sharing (e.g., Varian [2009], Jones and Tonetti [2018], Veldkamp et al. [2019], and Veldkamp [2019]).
Economists have recognized that consumers might have privacy concerns (e.g., Stigler [1980],
Posner [1981], and Varian [2009]), but have often argued that data markets could appropriately
balance privacy concerns and the social benefits of data (e.g., Laudon [1996] and Posner and Weyl
[2018]). In any case, the willingness of the majority of users to allow their data to be used for no
or very little direct benefits is argued to be evidence that most users place only a small value on
privacy.
2
This paper, in contrast, argues that there are forces that will make individual-level data under-
priced and the market economy generate too much data. The reason is simple: when an individual
shares her data, she compromises not only her own privacy but also the privacy of other individ-
uals whose information is correlated with hers. This negative externality tends to create excessive
data sharing. Moreover, when there is excessive data sharing, each individual will overlook her
privacy concerns and part with her own information because others’ sharing decisions will have
already revealed much about her.
Some of the issues we emphasize are highlighted by the Cambridge Analytica scandal. The
company acquired the private information of millions of individuals from data shared by 270,000
Facebook users who voluntarily downloaded an app for mapping their personality traits, called
“This is your digital life”. The app accessed users’ news feed, timeline, posts and messages, and
revealed information about other Facebook users. Cambridge Analytica was ultimately able to infer
valuable information about more than 50 million Facebook users, which it deployed for designing
personalized political messages and advertising in the Brexit referendum and 2016 US presidential
election.
3
Though some of the circumstances of this scandal are unique, the issues are general. For
example, when an individual shares information about his own behavior, habits and preferences,
this contains considerable information about the behavior, habits and preferences of not only his
friends but also other people with similar characteristics (e.g., the routines and choices of a highly-
educated gay from Central America in his early 20s in Somerville, Massachusetts is informative
1
Just Facebook has almost 2.5 billion monthly (active) individual users.
2
Consumers often report valuing privacy (e.g., Westin [1968]; Goldfarb and Tucker [2012]), but do not take much
action to protect their privacy (e.g., “Why your inbox is crammed full of privacy policies”, WIRED, May 24, 2018 and
Athey et al. [2017]).
3
See New York Times, March, 19 2018 and New York Times, March, 13, 2018, and The Guardian, April, 13, 2018
1
about others with the same profile and residing in the same area).
The following example illustrates the nature of the problem, introduces some of our key con-
cepts, and clarifies why there will be excessive data sharing and very little willingness to protect
privacy on the part of users.
Consider a platform with two users, i = 1, 2. Each user owns her own personal data, which
we represent with a random variable X
i
(from the viewpoint of the platform). The relevant data
of the two users are related, which we capture by assuming that their random variables are jointly
normally distributed with mean zero and correlation coefficient ρ. The platform can acquire or
buy the data of a user in order to better estimate her preferences or actions. Its objective is to
minimize the mean square error of its estimates of user types, or maximize the amount of leaked
information about them. Suppose that the valuation (in monetary terms) of the platform for the
users’ leaked information is one, while the value that the first user attaches to her privacy, again
in terms of leaked information about her, is 1/2 and for the second user it is v > 0. We also assume
that the platform makes take-it-or-leave-it offers to the users to purchase their data. In the absence
of any restrictions on data markets or transaction costs, the first user will always sell her data
(because her valuation of privacy, 1/2, is less than the value of information to the platform, 1).
But given the correlation between the types of the two users, this implies that the platform will
already have a fairly good estimate of the second user’s information. Suppose, for illustration,
that ρ ≈ 1. In this case, the platform will know almost everything relevant about user 2 from user
1’s data, and this undermines the willingness of user 2 to protect her data. In fact, since user 1 is
revealing almost everything about her, she would be willing to sell her own data for a very low
price (approximately 0 given ρ ≈ 1). But once the second user is selling her data, this also reveals
the first user’s data, so the first user can only charge a very low price for her data. Therefore in this
simple example, the platform will be able to acquire both users’ data at approximately zero price.
Critically, however, this price does not reflect the users’ valuation of privacy. When v ≤ 1, the
equilibrium is efficient because data are socially beneficial in this case (even if data externalities
change the distribution of economic surplus to the advantage of the platform). However, it can be
arbitrarily inefficient when v is sufficiently high. This is because the first user, by selling her data,
is creating a negative externality on the second user.
This simple example captures many of the economic ideas of the paper. Our formal analysis
generalizes these insights by considering a community of users whose information are correlated
in an arbitrary fashion and who have heterogeneous valuations of privacy. Finally, we analyze
this model both under a monopoly platform and under competition between platforms trying to
simultaneously attract users and acquire their data.
Our main results correspond to generalizations of the insights summarized by the preceding
example. First, we introduce our general framework and characterize the first-best allocation
which maximizes the sum of surplus of users and platforms. The first best typically involves
considerable data transactions, but those individuals creating significant (negative) externalities
on others should not share their data. Second, we establish the existence of an equilibrium and
2

characterize the prices at which data will be transacted. This characterization clarifies how the
market price of data for a user and the distribution of surplus depend on information leaked by
other users. Third and more importantly, we provide conditions under which the equilibrium in
the data market is inefficient as well as conditions for simple restrictions on markets to improve
welfare. At the root of these inefficiencies are the economic forces already highlighted by our
example: inefficiencies arise when a subset of users are willing to part with their data, which are
informative about other users whose value of privacy is high. We show that these insights extend
to environments with competing platforms and incomplete information as well.
We further investigate various policy approaches to data markets. Person-specific taxes on
data transactions can restore the first best, but are impractical. We show in addition how uniform
taxation on all data transactions might, under some conditions, improve welfare. Finally, we
propose a new regulation scheme where data transactions are mediated in a way that reduces their
correlation with the data of other users, thus minimizing leaked information about others. We
additionally develop a procedure for implementing this scheme based on “de-correlation”, meaning
transforming users’ data so that their correlation with others’ data and types is removed.
4
Our paper relates to the literature on privacy and its legal and economic aspects. The classic
definition of privacy, proposed by justices Warren and Brandeis in 1890, is the protection of some-
one’s personal space and the right to be let alone (Warren and Brandeis [1890]). Relatedly, and
more relevant to our focus, Westin [1968] defines it as the control over and safeguarding of per-
sonal information, and this perspective has been explored from various angles in recent work (e.g.,
Pasquale [2015], Tirole [2019], Zuboff [2019]). More closely related to our paper are MacCarthy
[2010], Fairfield and Engel [2015], Choi et al. [2019], and Bergemann et al. [2019]. MacCarthy
[2010] and Fairfield and Engel [2015] are the first contributions we are aware of that emphasize
externalities in data sharing, which play a central role in our analysis. More recently, Choi et al.
[2019] develop a reduced-form model with a related informational externality and a number of re-
sults similar to our excessive information sharing finding. There are several important differences
between this paper and ours, however. First, Choi et al. [2019] do not model how data sharing
creates an externality and simply assume that consumer welfare depends negatively on the num-
ber of other consumers on an online platform. In contrast, much of our analysis is devoted to the
study of how the correlation structure across different users jointly determines sharing decisions
and the amount of leaked information. Second, they assume that consumers are identical, while
our above example already illustrates that heterogeneity in privacy concerns plays a critical role
in the inefficiencies in data markets. Indeed, our analysis highlights that there are only limited
inefficiencies when all users are homogeneous (specifically, the equilibrium is efficient in this case
when they have low or sufficiently high value of privacy). Third, their paper does not analyze
the case with competing platforms. Finally, Bergemann et al. [2019] also study an environment
with data externalities. Though there are some parallels between the two papers, their work is
4
This de-correlation procedure is different from anonymization of data because it does not hide information about
the user sharing her data but about others who are correlated with this user.
3
different from and largely complementary to ours. In particular, they analyze an economy with
symmetric users where there is a monopolist platform and data are used by this monopolist or
other downstream firms (such as advertisers) for price discrimination. They focus on the impli-
cations for market prices, profits, and efficiency of the structure of the downstream market and
whether data are collected in an anonymized or non-anonymized form.
Our paper also relates to the growing literature on information markets. One branch of this
literature focuses on the use of personal data for improved allocation of online resources (e.g.,
Bergemann and Bonatti [2015], Goldfarb and Tucker [2011], and Montes et al. [2018]). Another
branch investigates how information can be monetized either by dynamic sales or optimal mech-
anisms. For example, Anton and Yao [2002], Babaioff et al. [2012], Es
˝
o and Szentes [2007], Horner
and Skrzypacz [2016], Bergemann et al. [2018], and Eliaz et al. [2019] consider either static or dy-
namic mechanisms for selling data, Ghosh and Roth [2015] uses differential privacy framework
of Dwork and Roth [2014] and study mechanism design with privacy constraints, and Admati
and Pfleiderer [1986] and Begenau et al. [2018] study markets for financial data. A third branch
focuses on optimal collection and acquisition of information, for example, Agarwal et al. [2018],
Chen and Zheng [2018], and Chen et al. [2018]. Lastly, a number of papers investigate the ques-
tion of whether information harms consumers, either because users are unaware of the data being
collected about them (Taylor [2004]) or because of price discrimination related reasons (Acquisti
and Varian [2005]). See Acquisti et al. [2016], Bergemann and Bonatti [2019], and Agrawal et al.
[2018] for excellent surveys of different aspects of this literature.
The rest of the paper proceeds as follows. Section 2 presents our model, focusing on the case
with a single platform for simplicity. Section 3 provides our main results, in particular, charac-
terizing the structure of equilibria in data markets and highlighting their inefficiency due to data
externalities. It also shows how shutting down data markets may improve welfare. Section 4
extends these results to a setting with competing platforms, while Section 5 presents analogous
results when the value of privacy of each user is their private information. Section 6 shows that
two types of policies, taxes and third-party-mediated information sharing, can improve welfare.
Section 7 concludes, while Appendix A presents the proofs of some of the results stated in the text
and the online Appendix B contains the remaining proofs and additional results.
2 Model
In this section we introduce our model, focusing first on the case with a single platform. Compe-
tition between platforms is analyzed in Section 4.
2.1 Information and Payoffs
We consider n users represented by the set V = {1, . . . , n}. Each user i ∈ V has a type denoted by
x
i
which is a realization of a random variable X
i
. We assume that the vector of random variables
X = (X
1
, . . . , X
n
) has a joint normal distribution N (0, Σ), where Σ ∈ R
n×n
is the covariance
4

matrix of X. Let Σ
ij
designate the (i, j)-th entry of Σ and Σ
ii
= σ
2
i
> 0 denote the variance of
individual i’s type.
Each user has some personal data, S
i
, which is informative about her type (for example, based
on her past behavior, preferences, or contacts). We suppose that S
i
= X
i
+ Z
i
where Z
i
is an
independent random variable with standard normal distribution, i.e., Z
i
∼ N (0, 1).
For any user joining the platform, the platform can derive additional revenue if it can predict
her type. This might be because of improved personalized services, targeted advertising, or price
discrimination for some services sold on the platform. Since the exact source of revenue for the
platform is immaterial for our analysis, we simply assume that the platform’s revenue from each
user is a(n inverse) function of the mean square error of its forecast of the user’s type, minus what
the platform pays to users to acquire their information. Namely, the objective of the platform is to
minimize
X
i∈V
E
h
(ˆx
i
(S) − X
i
)
2
i
− σ
2
i
+ p
i
, (1)
where S is the vector of data the platform acquires, ˆx
i
(S) is the platform’s estimate of the user’s
type given this information, −σ
2
i
is included as a convenient normalization, and p
i
denotes pay-
ments to user i from the platform (we ignore for simplicity any other transaction costs incurred
by the platform and discuss taxes and regulations in Section 6). This payment to the user may be
a direct one in an explicit data market or it may be an implicit transfer, for example, in the form of
some good or service the platform provides to the user in exchange for her data.
Users value their privacy, which we also model in a reduced-form manner as a function of the
same mean square error.
5
This reflects both pecuniary and nonpecuniary motives, for example,
the fact that a user may receive a greater consumer surplus when the platform knows less about
her or she may have a genuine demand for keeping her preferences, behavior, and information
private. There may also be political and social reasons for privacy, for example, for concealing
dissident activities or behaviors disapproved by some groups. We assume, specifically, that user
i’s value of privacy is v
i
≥ 0, and her payoff is
v
i
E
h
(ˆx
i
(S) − X
i
)
2
i
− σ
2
i
+ p
i
.
This expression and its comparison with (1) clarifies that the platform and users have potentially-
opposing preferences over information about user type. We have again subtracted σ
2
i
as a normal-
ization, which ensures that if the platform acquires no additional information about the user and
makes no payment to her, her payoff is zero.
Critically, users with v
i
< 1 value their privacy less than the valuation that the platform at-
taches to information about them, and thus reducing the mean square error of the estimates of
their types is socially beneficial. In contrast, users with v
i
> 1 value their privacy more, and
5
In this and the next section, we do not model the decision of whether to join the platform. Joining decisions are
introduced in Section 4, where we assume that users receive additional services (unrelated to their personal data) from
platforms encouraging them to join even in the presence of loss of privacy.
5
reducing their mean square error is socially costly. In a world without data externalities (where
data about one user have no relevance to the information about other users), the first group of
users should allow the platform to acquire (buy) their data, while the second group should not. A
simple market mechanism based on prices for data can implement this efficient outcome.
We will see that the situation is very different in the presence of data externalities.
2.2 Leaked Information
A key notion for our analysis is leaked information, which captures the reduction in the mean square
error of the platform’s estimate of the type of a user. When the platform has no information about
user i, its estimate satisfies E
h
(ˆx
i
− X
i
)
2
i
= σ
2
i
. As the platform receives data from this and other
users, its estimate improves and the mean square error declines. The notion of leaked information
captures this reduction in mean square error.
Specifically, let a
i
∈ {0, 1} denote the data sharing action of user i ∈ V with a
i
= 1 correspond-
ing to sharing. Denote the profile of sharing decisions by a = (a
1
, . . . , a
n
) and the decisions of
agents other than i by a
−i
. We also use the notation S
a
to denote the data of all individuals for
whom a
j
= 1, i.e., S
a
= (S
j
: j ∈ V s.t. a
j
= 1). Given a profile of actions a, the leaked information
of (or about) user i ∈ V is the reduction in the mean square error of the best estimator of the type
of user i:
I
i
(a) = σ
2
i
− min
ˆx
i
E
h
(X
i
− ˆx
i
(S
a
))
2
i
.
Notably, because of data externalities, leaked information about user i depends not just on her
decisions but also on the sharing actions taken by all users.
With this notion at hand, we can write the payoff of user i given the price vector p = (p
1
, . . . , p
n
)
as
u
i
(a
i
, a
−i
, p) =
p
i
− v
i
I
i
(a
i
= 1, a
−i
) , a
i
= 1
−v
i
I
i
(a
i
= 0, a
−i
) , a
i
= 0,
where recall that v
i
≥ 0 is user’s value of privacy.
We also express the platform’s payoff more compactly as
U(a, p) =
X
i∈V
I
i
(a) −
X
i∈V: a
i
=1
p
i
. (2)
2.3 Equilibrium Concept
An action profile a = (a
1
, . . . , a
n
) and a price vector p = (p
1
, . . . , p
n
) constitute a pure strategy
equilibrium if both users and the platform maximize their payoffs given other players’ strategies.
More formally, in the next definition we define an equilibrium as a Stackelberg equilibrium in which
the platform chooses the price vector recognizing the user equilibrium that will result following this
choice.
6

Definition 1. Given the price vector p = (p
1
, . . . , p
n
), an action profile a = (a
1
, . . . , a
n
) is user
equilibrium if for all i ∈ V,
a
i
∈ argmax
a∈{0,1}
u
i
(a
i
= a, a
−i
, p).
We denote the set of user equilibria at a given price vector p by A(p). A pair (p
E
, a
E
) of price and
action vectors is a pure strategy Stackelberg equilibrium if a
E
∈ A(p
E
) and there is no profitable
deviation for the platform, i.e.,
U(a
E
, p
E
) ≥ U(a, p), for all p and for all a ∈ A(p).
In what follows, we refer to a pure strategy Stackelberg equilibrium simply as an equilibrium.
3 Analysis
In this section, we first study the first-best information sharing decisions that maximize the sum of
users and platform payoffs and then proceed to characterizing the equilibrium and its efficiency
properties.
3.1 First Best
We define the first best as the data sharing decisions that maximize utilitarian social welfare or
social surplus given by the sum of the payoffs of the platform and users. Social surplus from an
action profile a is
Social surplus(a) = U(a, p) +
X
i∈V
u
i
(a, p) =
X
i∈V
(1 − v
i
)I
i
(a).
Prices do not appear in this expression because they are transfers from the platform to users.
6
The
first-best action profile, a
W
, maximizes this expression. The next proposition characterizes the
first-best action profile.
Proposition 1. The first best involves a
W
i
= 1 if
X
j∈V
(1 − v
j
)
Cov
X
i
, X
j
| a
i
= 0, a
W
−i
2
1 + σ
2
j
− I
j
(a
i
= 0, a
W
−i
)
≥ 0, (3)
and a
W
i
= 0 if the left-hand side of (3) is negative.
The proof of this proposition as well as all other proofs, unless otherwise stated, are presented
in Appendix A.
6
In including the platform’s payoff in social surplus we are assuming that this payoff is not coming from shifting
revenues from some other (perhaps off-line) businesses. If we do not include the payoff of the platform in our welfare
measure, our inefficiency results would hold a fortiori.
7

To understand this result, consider first the case in which there are no data externalities so that
the covariance terms in (3) are zero, except Cov
X
i
, X
i
| a
i
= 0, a
W
−i
= σ
2
i
, so that the left-hand
side is simply σ
4
i
/(1 + σ
2
i
) times 1 − v
i
. This yields a
W
i
= 1 if v
i
≤ 1. The situation is different in
the presence of data externalities, because now the covariance terms are non-zero. In this case, an
individual should optimally share her data only if it does not reveal too much about users with
v
j
> 1.
3.2 Equilibrium Preliminaries
The next lemma characterizes two important properties of the leaked information function I
i
:
{0, 1}
n
→ R.
Lemma 1. 1. Monotonicity: for two action profiles a and a
0
with a ≥ a
0
,
I
i
(a) ≥ I
i
(a
0
), ∀i ∈ {1, . . . , n}.
2. Submodularity: for two action profiles a and a
0
with a
0
−i
≥ a
−i
,
I
i
(a
i
= 1, a
−i
) − I
i
(a
i
= 0, a
−i
) ≥ I
i
(a
i
= 1, a
0
−i
) − I
i
(a
i
= 0, a
0
−i
).
The monotonicity property states that as the set of users who share their information expands,
the leaked information about each user (weakly) increases. This is an intuitive consequence of
the fact that more information always facilitates the estimation problem of the platform and re-
duces the mean square error of its estimates. More important for the rest of our analysis is the
submodularity property, which implies that the marginal increase in the leaked information from
individual i’s sharing decision is decreasing in the information shared by others. This too is intu-
itive and follows from the fact that when others’ actions reveal more information, there is less to
be revealed by the sharing decision of any given individual.
7
Using Lemma 1 we next show that for any price vector p ∈ R
n
, the set A(p) is a (non-empty)
complete lattice.
Lemma 2. For any p, the set A(p) is a complete lattice, and thus has a least and a greatest element.
Lemma 2 implies that the set of user equilibria is always non-empty, but may not be singleton
as we illustrate in the next example.
7
Lemma 1 is established under the assumption of Gaussian signals and with mean square error as the measure of
leaked information the players care about. However, this lemma and our equilibrium existence and inefficiency results
that build on it hold for any structure of signals and any measure of leaked information that ensure the monotonicity
and submodularity properties of Lemma 1. One important example that satisfies these properties is a leaked infor-
mation measure given by the mutual information between a user’s type and the vector of types of users who have
shared their data: I
i
(a) = I(X
i
; (X
j
: a
j
= 1)) (where the mutual information between two random variables X
and Y is defined as I (X ; Y ) = E
X,Y
[− log
P (X )P (Y )
P (X,Y )
]). This measure of leaked information satisfies monotonicity and
submodularity for any distribution of random variables X (see Appendix B for more details).
8

1
2
1
2
1
2
1
2
(2−ρ
2
)
2
2(4−ρ
2
)
(2−ρ
2
)
2
2(4−ρ
2
)
(2−ρ
2
)
2
2(4−ρ
2
)
(2−ρ
2
)
2
2(4−ρ
2
)
a
1
=1a
1
=1
a
1
=1a
1
=1
a
2
=0a
2
=0
a
1
=0a
1
=0
a
2
=1a
2
=1
p
2
p
2
p
1
p
1
a
2
=0a
2
=0
a
1
=0a
1
=0
a
2
=1a
2
=1
Figure 1: The user equilibrium as a function of price vector (p
1
, p
2
) in the setting of Example 1. For
the prices in the purple area in the center, both a
1
= a
2
= 0 and a
1
= a
2
= 1 are user equilibria.
Example 1. Suppose there are two users 1 and 2 with covariance matrix
Σ =
1 ρ
ρ 1
!
and v
1
= v
2
= v. The set of user equilibria in this case is depicted in Figure 1. When p
1
, p
2
∈
h
(2−ρ
2
)
2
2(4−ρ
2
)
,
1
2
i
, both action profiles a
1
= a
2
= 0 and a
1
= a
2
= 1 are user equilibria. This is a
consequence of the submodularity of the leaked information function (Lemma 1): when user 1
shares her data, she is also revealing a lot about user 2, and making it less costly for her to share
her data. Conversely, when user 1 does not share, this encourages user 2 not to share. Despite this
multiplicity of user equilibria, there exists a unique (Stackelberg) equilibrium for this game given
by a
E
1
= a
E
2
= 1 and p
E
1
= p
E
2
=
(2−ρ
2
)
2
2(4−ρ
2
)
. This uniqueness follows because the platform can choose
the price vector to encourage both users to share.
3.3 Existence of Equilibrium
The next theorem establishes the existence of a (pure strategy) equilibrium.
Theorem 1. An equilibrium always exists. That is, there exist an action profile a
E
and a price vector p
E
such that a
E
∈ A(p
E
), and
U(a
E
, p
E
) ≥ U(a, p), for all p and for all a ∈ A(p). (4)
Note that the equilibrium may not be unique, but if there are multiple equilibria, all of them
yield the same payoff for the platform (since otherwise (4) would not be satisfied for the equilib-
rium with lower payoff for the platform). The following example clarifies this point.
9

Example 2. Suppose there are three users with the same value of privacy and variance: v
i
= 1.18
and σ
2
i
= 1 for i = 1, 2, 3. We let all off-diagonal entries of Σ to be 0.3. Any action profile where
two out of three users share their information is an equilibrium, and thus there are three distinct
equilibria. But it is straightforward to verify that they all yield the same payoff to the platform.
3.4 An Illustrative Example
In this subsection, we provide an illustrative example that shows how some of the key objects in
our analysis are computed and highlights a few of the subtle aspects of the equilibrium. Consider
the same setting as in Example 1 with two users with the same value of privacy, v, and a correlation
coefficient ρ between their information. Given the action profile of users, the joint distribution of
(X
1
, S
1
, S
2
) in this example is
X
1
S
1
S
2
∼ N
0
0
0
,
1 1 ρ
1 1 + γ
2
1
ρ
ρ ρ 1 + γ
2
2
,
where
γ
2
i
=
1 a
i
= 1,
∞ a
i
= 0.
Suppose the platform has received the signals (S
1
, S
2
), then its optimal estimator for X
1
, ˆx
1
(S
1
, S
2
),
is simply the conditional expectation of X
1
given s
1
and s
2
, and its mean square error is equal to
this estimator’s variance, i.e.,
min
ˆx
1
E
h
(ˆx
1
(S
1
, S
2
) − X
1
)
2
i
=
γ
2
1
(1 + γ
2
2
− ρ
2
)
(1 + γ
2
1
)(1 + γ
2
2
) − ρ
2
.
Similarly, the mean square error of the platform’s best estimator for X
2
is
min
ˆx
2
E
h
(ˆx
2
(S
1
, S
2
) − X
2
)
2
i
=
γ
2
2
(1 + γ
2
1
− ρ
2
)
(1 + γ
2
1
)(1 + γ
2
2
) − ρ
2
.
We first show that the total payment from the platform to users is non-monotone in the number
of users sharing their information. When the platform induces both users to share (a
1
= a
2
= 1),
it makes a total payment of v
(2−ρ
2
)
2
4−ρ
2
. In contrast, when it only induces the first user to share
(a
1
= 1, a
2
= 0), this will cost
v
2
. Therefore, when ρ
2
≥
7−
√
17
4
≈ 0.71, the platform pays less to
have both users share their data. Intuitively, this cost-saving for the platform is a consequence of
the submodularity of leaked information (Lemma 1): when both users share, the data of each are
less valuable in view of the information revealed by the other user. This finding reflects one of the
claims made in the Introduction: market prices for data do not reflect the value that users attached
to their privacy and may be depressed because of data externalities.
We next illustrate that equilibrium (social) surplus is non-monotonic in the users’ value of
10
11
4
(2−ρ
2
)
2
4
(2−ρ
2
)
2
vv
a
E
1
= a
E
2
=1a
E
1
= a
E
2
=1 a
E
1
= a
E
2
=0a
E
1
= a
E
2
=0
Social surplusSocial surplus
4
4−ρ
2
4
4−ρ
2
Figure 2: Equilibrium and social surplus as a function of the value of privacy v for a setting with
two users with σ
2
1
= σ
2
2
= 1, Σ
12
= ρ, and v
1
= v
2
= v.
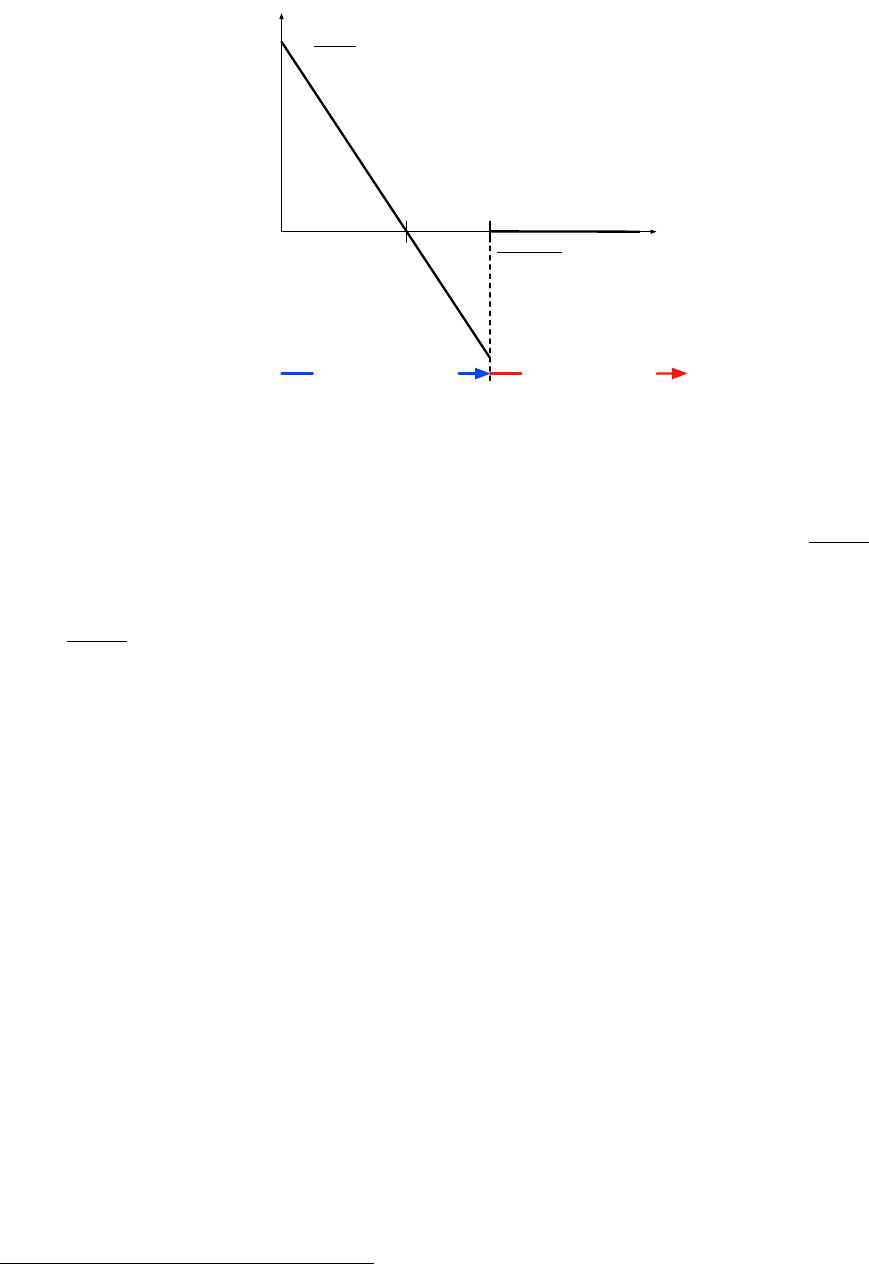
privacy. Equilibrium surplus is depicted in Figure 2. For values of v larger than
4
(2−ρ
2
)
2
, users
do not share their data and equilibrium surplus is zero. When v is smaller than 1, users share
their data and equilibrium surplus is positive. For intermediate values of v, in particular for
v ∈ [1,
4
(2−ρ
2
)
2
], the platform chooses a price vector that induces both users to share their data, but
in this case, the social surplus is negative. The intuition is related to the point already emphasized
in the previous paragraph: when both users share their data, the externalities depress the market
prices for data and this makes it profitable for the platform to acquire the users’ data even though
v > 1. More explicitly, when user 2 shares her data, this reveals sufficient information about user
1 that she becomes willing to accept a relatively low price for sharing her data, and this maintains
an equilibrium with low prices for data even though both users attach a relatively high value to
their privacy.
3.5 Equilibrium Prices
In this subsection, we characterize the equilibrium price vector. For any action profile a ∈ {0, 1}
n
,
let p
a
denote the least (element-wise minimum) equilibrium price vector that sustains an action
profile a in a user equilibrium. More specifically, p
a
is defined such that:
8
p
a
≤ p, for all p such that a ∈ A(p).
Profit maximization by the platform implies that equilibrium prices must satisfy this property —
since otherwise the platform could reduce prices and still implement the same action profile. We
therefore refer to p
a
as “equilibrium price vector” or simply as “equilibrium prices” (with the
8
Prices for users not sharing their data are not well-defined.
11

understanding that these would be the equilibrium prices when the platform chooses to induce
action profile a).
The next theorem computes this price vector (and shows that it exists).
Theorem 2. For any action profile a ∈ {0, 1}
n
, we have
I
i
(a
i
= 1, a
−i
) = I
i
(a
i
= 0, a
−i
) +
σ
2
i
− I
i
(a
i
= 0, a
−i
)
2
(σ
2
i
+ 1) − I
i
(a
i
= 0, a
−i
)
, (5)
and
I
i
(a
i
= 0, a
−i
) = d
T
i
(I + D
i
)
−1
d
i
, for all a
i
= 1,
where D
i
is the matrix obtained by removing row and column i from matrix Σ as well as all rows and
columns j for which a
j
= 0, and d
i
is (Σ
ij
: j s.t. a
j
= 1). The equilibrium price that sustains action
profile a is
p
a
i
=
v
i
(
σ
2
i
−I
i
(a
i
=0,a
−i
)
)
2
(σ
2
i
+1)−I
i
(a
i
=0,a
−i
)
, a
i
= 1,
0, a
i
= 0.
The first part of Theorem 2 provides a decomposition of leaked information about user i in
terms of leaked information about her when she does not share her data. In particular, the first
term on the right-hand side of the equation (5), I
i
(a
i
= 0, a
−i
), is her leaked information resulting
from the data sharing of other users and thus represents the data externality. The second term
is the additional leakage when user i shares her data. The second part of Theorem 2 states that
the equilibrium price offered to any user i who shares her information must make her indifferent
between sharing and not sharing. This is because prices are determined by the platform’s offers.
This is also why the equilibrium price, p
a
i
, is equal to the value of privacy, v
i
, multiplied by the
second term in (5), which is the additional leakage of information and hence the loss of privacy
resulting from the user’s own data sharing.
The following is an immediate corollary of Theorem 2.
Corollary 1. For any user i, the equilibrium price p
(a
i
=1,a
−i
)
i
(that induces a
i
= 1 for any action profile
a
−i
∈ {0, 1}
n−1
) is increasing in σ
2
i
and decreasing in the data externality captured by I
i
(a
i
= 0, a
−i
).
Moreover, leaked information I
i
(a
i
= 1, a
−i
) is increasing in σ
2
i
and in the data externality I
i
(a
i
= 0, a
−i
).
The first part of Corollary 1 shows that a higher variance of user’s type, σ
2
i
, increases the
equilibrium price. Intuitively, a higher variance makes the user’s type more difficult to predict
and thus her own information more valuable. This also explains why the price is decreasing in the
data externality — represented by information leaked by others, I
i
(a
i
= 0, a
−i
). The last part of
Corollary 1 shows that a higher variance of individual type, as well as a greater data externality,
increase the overall leakage of information about the user.
The next proposition establishes that greater correlation between users’ data, and thus greater
data externality, reduces equilibrium prices.
12

Proposition 2. For any action profile a ∈ {0, 1}
n
and any i ∈ V, the price p
a
i
is nonincreasing in the
absolute value of the covariance between any pair of users given the action profile a.
The equilibrium price for i is the difference between the information that platform has about
i with and without i’s own data (multiplied by her value of privacy v
i
). Suppose first that the
correlation between i’s data and some other user j’s data increases. Mathematically, this means
that |Cov(X
i
, X
j
| a)| increases, and user j’s information about i becomes more accurate. There-
fore, provided that a
j
= 1, this reduces the value of user i’s information for predicting her type
and thus depresses her benefits from protecting her data. The same result also applies when the
correlation between two other users increases, that is, when |Cov(X
j
, X
k
| a)| increases. In this
case, the platform obtains more accurate information about users j and k, and indirectly their data
become more informative about user i, leading to the same conclusion.
Proposition 2 establishes that equilibrium prices are nonincreasing in the correlation between
users’ data. Yet the number of users who share their data in equilibrium is non-monotone in this
correlation as we show in the next example.
Example 3. Consider a setting with three users with Σ
12
= Σ
13
= 1/2, Σ
23
= ρ, v
i
= 3/2, and
σ
2
i
= 1 for all users. We have the following cases.
1. ρ = 0: the equilibrium decisions are a
1
= 1, and a
2
= a
3
= 0, the total payment is 0.75, and
the total information leakage is
P
3
i=1
I
i
(a
E
) = 0.75.
2. ρ = 1/2: the equilibrium decisions are a
1
= a
2
= a
3
= 1, the total payment is 1.6, and the
total information leakage is
P
3
i=1
I
i
(a
E
) = 1.66.
3. ρ = 1: the equilibrium decisions are a
1
= 0 and a
2
= a
3
= 1, the total payment is 0.5, and
the total information leakage is
P
3
i=1
I
i
(a
E
) = 1.5.
Therefore, as we increase the correlation among users, the set of users that share information in
equilibrium may increase (from case 1 to case 2) or decrease (from case 2 to case 3). The intuition
is that as more information is leaked about a user (in this case about user 1), the value of her data
both to the platform and to herself declines, and the platform may no longer find it worthwhile to
compensate her for selling her data.
The next proposition, however, shows that equilibrium prices are decreasing in the set of users
sharing their data.
Proposition 3. For two action profiles a, a
0
with a
0
≥ a, we have p
a
0
i
≤ p
a
i
for all i ∈ V for which a
i
= 1.
Proposition 3 follows from Theorem 2 and Lemma 1. In particular, using Theorem 2 the equi-
librium price for user i is her additional loss of privacy (increase in the information leakage multi-
plied by v
i
) if she shares her data. From the submodularity of information leakage (Lemma 1) the
additional information the user leaks about herself decreases when more people share their data.
9
9
The proposition covers the prices for users sharing their data, since prices for those not sharing are not well-defined.
13

3.6 Inefficiency
This subsection presents one of our main results, documenting the extent of inefficiency in data
markets.
First note that all users with value of privacy less than 1 will always share their data in equi-
librium. For future reference, we state this straightforward result as a lemma.
Lemma 3. All users with value of privacy v
i
≤ 1 share their data in equilibrium.
10
Motivated by this lemma, we partition users into two sets, those with value of privacy below
1 (“low-value users”) and those above (“high-value users”):
V
(l)
= {i ∈ V : v
i
≤ 1} and V
(h)
= {i ∈ V : v
i
> 1}.
We also denote by v
(h)
and v
(l)
the vectors of valuations of privacy for high-value and low-value
users, respectively. Lemma 3 then implies that for all i ∈ V
(l)
we have a
E
i
= 1.
The next theorem provides conditions for efficiency and inefficiency. More precisely, we show
that if every high-value user is uncorrelated with all other users, then equilibrium is efficient.
Otherwise, if either a high-value user is correlated with a low-value user or two high-value users
are correlated, there exists a set of valuations (consistent with the set of high and low-value users)
such that any equilibrium is inefficient.
Theorem 3. 1. Suppose every high-value user is uncorrelated with all other users. Then the equilib-
rium is efficient.
2. Suppose at least one high-value user is correlated (has a non-zero correlation coefficient) with a low-
value user. Then there exists
¯
v ∈ R
|V
(h)
|
such that for v
(h)
≥
¯
v the equilibrium is inefficient.
3. Suppose every high-value user is uncorrelated with all low-value users and at least one high-value
user is correlated with another high-value user. Let
˜
V
(h)
⊆ V
(h)
be the subset of high-value users
correlated with at least one other high-value user. Then for each i ∈
˜
V
(h)
there exists ¯v
i
> 0 such that
if for any i ∈
˜
V
(h)
v
i
< ¯v
i
, the equilibrium is inefficient
Theorem 3 clarifies the source of inefficiency in our model. If high-value users are not cor-
related with others, the equilibrium is efficient. In this case, there may still be data externalities
among low-value users and these may affect market prices (and the distribution of economic gains
between the users and the platform). But they do not create a loss of privacy for users who prefer
not to share their data.
10
The only subtlety here is about users with v
i
= 1. If these users’ information is correlated with others who are
already sharing, their equilibrium price will be strictly less than 1, and this will make it strictly beneficial for the
platform to purchase their data. If they are correlated with others who are not sharing, then the platform would still
like to purchase these data because of the additional reduction in the mean square error of its estimates of others’
types they enable. When such an individual is uncorrelated with anybody else, then the platform would be indifferent
between purchasing her data and not. In this case, for simplicity of notation, we suppose that it still purchases.
14
However, the second part of the theorem shows that if high-value users are correlated with
low-value users, the equilibrium is typically inefficient. The additional condition v
(h)
≥
¯
v is not
a restrictive one as highlighted in Example 4 below and rules out cases in which high-value users
suffer only little loss of privacy but generate socially valuable information about low-value users.
In general, the inefficiency identified in this part of the theorem can take one of two forms: either
high-value users do not share their data, but because of information leaked about them, they suffer
a loss of privacy. Or given the amount of leaked information about them, high-value users decide
to share themselves (despite their initial reluctance to do so).
Finally, the third part of the theorem covers the remaining case, where high-value users are
uncorrelated with low-value users but are correlated among themselves. The equilibrium is again
inefficient, because the platform can induce some of them to share their data (even though indi-
vidually each would prefer not to). This is because when a subset of them share, this compromises
the privacy of others, depresses data prices, and may incentivize them to share too (in turn further
depressing data prices). This inefficiency applies when some high-value users have intermediate
values of privacy (i.e., v
i
∈ (1, ¯v
i
)), since those with sufficiently high value of privacy cannot be
induced to share their data.
Overall, this theorem highlights that inefficiency in data markets originates from the combina-
tion of sufficiently high value attached to privacy by some users and their correlation with other
users. It therefore emphasizes that inefficiency in our model is tightly linked to data externalities.
3.7 Are Data Markets Beneficial?
Theorem 3 focuses on the comparison of the market equilibrium to the first best. This is a tough
comparison for the market because in the first best some users share their data and benefit from
market transactions, while others do not share. A lower bar for data markets is whether they
achieve positive social surplus so that any inefficiencies they create are (partially) compensated
by benefits for other agents. We next show that this is not necessarily the case and provide a
sufficient condition for the equilibrium (social) surplus to be negative — so that shutting down
data markets all together would improve social surplus (and thus utilitarian welfare). Let us also
introduce the following notation: for any action profile a ∈ {0, 1}
n
, we let I
i
(T ) denote the leaked
information about user i where T = {i ∈ V : a
i
= 1}.
Proposition 4. We have
Social surplus(a
E
) ≤
X
i∈V
(l)
(1 − v
i
)I
i
(V) −
X
i∈V
(h)
(v
i
− 1)I
i
(V
(l)
).
This implies that if
X
i∈V
(h)
(v
i
− 1)I
i
(V
(l)
) >
X
i∈V
(l)
(1 − v
i
)I
i
(V), (6)
then the equilibrium surplus is negative and utilitarian welfare improves if data markets are shut down.
15

This proposition follows immediately from Lemma 3. The first term is an upper bound on
the gain in social surplus from the sharing decisions of low-value users (even if these gains do
not necessarily accrue to the users themselves and are mainly captured by the platform). This
expression is an upper bound because we are evaluating this term under the assumption that all
users share their data, thus maximizing the amount of socially beneficial information about low-
value users. The second term is a lower bound on the loss of privacy from high-value users. It is a
lower bound because the loss of privacy is evaluated for the minimal set of agents, the low-value
ones, who always share their data (in equilibrium a superset of V
(l)
will share their data).
We also add that leaked information in this proposition is only a function of the matrix Σ as
shown in Theorem 2, so the right-hand side is in terms of model parameters and does not depend
on equilibrium objects.
The next proposition provides a sufficient condition in terms of values of privacy and corre-
lations between data that ensures condition (6) and implies that the equilibrium necessarily has
negative social surplus.
Proposition 5. Suppose
X
i∈V
(h)
(v
i
− 1)
P
j∈V
(l)
Σ
2
ij
||Σ
(l)
||
1
+ 1
!
>
X
i∈V
(l)
(1 − v
i
),
where ||Σ
(l)
||
1
denotes the 1-norm of the submatrix of Σ which only includes the rows and columns corre-
sponding to low-value users. Then the equilibrium surplus is negative.
11
Proposition 5 provides explicit sufficient conditions in terms of the values of privacy and the
correlation between high and low-value users for negative equilibrium surplus.
Example 4. We consider a setting with two communities, each of size 10. Suppose that all users in
community 1 are low-value and have a value of privacy equal to 0.9, while all users in community
2 are high-value (with v
h
> 1). We also take the variances of all user data to be 1, the correlation
between any two users who belong to the same community to be 1/20, and the correlation be-
tween any two users who belong to different communities to be ρ. Figure 3 depicts equilibrium
surplus as a function of v
h
and ρ. The curve in the figure represents the combinations of these two
variables for which the social surplus is equal to zero. Moving in the northeast direction reduces
equilibrium surplus and hence the shaded area has negative surplus. Consequently, in this part of
the parameter space, shutting down data markets improves utilitarian social welfare.
Two points are worth noting. First, relatively small values of the correlation coefficient ρ are
sufficient for social surplus to be negative. Second, when v
h
is very close to 1, the social surplus is
always positive because the negative surplus from high-value users is compensated by the social
benefits their data sharing creates for low-value users.
11
1-norm of a matrix A is defined as ||A||
1
= max
i
P
n
j=1
|A
ij
|.
16

Value of privacy for high-value users: v
h
12345678910
Cross-community correlation: ρ
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
Figure 3: Shaded area shows the pairs of (ρ, v
h
) with negative equilibrium surplus in the setting
of Example 4.
4 Competition Among Platforms
In this section we generalize the main results from the previous section to a setting in which
multiple platforms compete for (the data of) users. For simplicity we focus on the case in which
there are two platforms. Formally, we are dealing with a three-stage game in which first users
decide which platform to join (if any), then platforms simultaneously offer prices for data, and
then finally all users simultaneously decide whether to share their data. We start by assuming
that data externalities are only among users joining the same platform, but then generalize this to
the case in which the platform learns valuable information about users that are not on its platform
as well. At the end of the section, we also discuss the case in which platforms first set prices for
data in order to attract users.
4.1 Information and Payoffs
For any i ∈ V, we denote by b
i
∈ {0, 1, 2} the joining decision of user i in the first-stage game
where b
i
= 0 means user i does not join, b
i
= 1 means she joins platform 1, and b
i
= 2 stands for
joining platform 2. Let us also define
J
1
= {i ∈ V : b
i
= 1} and J
2
= {i ∈ V : b
i
= 2},
as the sets of users joining the two platforms.
Similar to the monopoly case in the previous section, the payoff of a platform is a function of
leaked information about users and payments to users. So for platform k ∈ {1, 2}, we have
U
(k)
(J
k
, a
J
k
, p
J
k
) =
X
i∈J
k
I
i
(a
J
k
) −
X
i∈J
k
: a
J
k
i
=1
p
J
k
i
, (7)
where a
J
k
∈ {0, 1}
|J
k
|
denotes the sharing decision of users belonging to this platform, and p
J
k
17
denotes the vector of prices the platform offers to users in J
k
.
The payoff of a user has three parts. First, each user receives a valuable service from the
platform it joins. Since we are modeling joining decisions in this section, we will be more explicit
about this “joining value” and assume that it depends on who else joins the platform. We therefore
write this part of the payoff as c
i
(J
b
i
) for user i joining platform b
i
, with the convention that J
0
= ∅,
and also normalize c
i
(J) = 0 for all J 63 i and for all i ∈ V. Second, the user suffers a disutility due
to loss of privacy from leaked information as before, and we again denote the value of privacy
for user i by v
i
. Third, she receives benefits from any payments from the platform in return of the
data she shares. Thus the payoff to user i joining platform k ∈ {1, 2} can be written as
u
i
(J
k
, a
i
, a
J
k
−i
, p
J
k
) =
p
J
k
i
− v
i
I
i
a
i
= 1, a
J
k
−i
+ c
i
(J
k
), a
i
= 1,
−v
i
I
i
a
i
= 0, a
J
k
−i
+ c
i
(J
k
) a
i
= 0.
With our convention, when the user chooses b
i
= 0, this payoff is equal to zero — there is no data
sharing decision, the payment is equal to zero, leaked information is equal to zero, and c
i
(∅) = 0.
The timing of events is as follows.
1. Users simultaneously decide which platform, if any, to join, i.e., b ={b
i
}
i∈V
, which deter-
mines J
1
and J
2
.
2. Given J
1
and J
2
, the two platforms simultaneously offer price vectors p
J
1
and p
J
2
.
3. Given J
1
and J
2
and p
J
1
and p
J
2
, users simultaneously make their data sharing decisions,
a : {0, 1, 2}
n
× R
n
→ {0, 1}.
The assumption that users join platforms before prices is adopted both for simplicity and to
capture the fact that there is currently a limited ability for platforms to attract customers by of-
fering prices for data. We discuss this type of price competition and its implications below. Even
though prices are offered at the second stage, users will anticipate these prices and the implica-
tions they have for leaked information in making their joining decisions.
4.2 Equilibrium Concept
We first observe that from the second stage on, once the set of users joining a platform is deter-
mined, this game is identical to the one we analyzed in the previous section. Hence, the Stackel-
berg equilibrium from the second stage onwards is defined analogously. Then in the first stage,
we define a joining equilibrium, as a profile of joining decisions anticipating the equilibrium from
the second stage onward. More formally:
Definition 2. Given a joining decision b and the corresponding sets of users on the two platforms,
J
1
and J
2
, a pure strategy Stackelberg equilibrium from the second stage onwards is given by price
18
vectors p
J
1
,E
and p
J
2
,E
and action profiles (a
J
1
,E
, a
J
2
,E
) such that a
J
k
,E
∈ A(p
J
k
,E
) and
U
(k)
(J
k
, a
J
k
,E
, p
J
k
,E
) ≥ U
(k)
(J
k
, a
J
k
, p
J
k
), for all p
J
k
and for all a
J
k
∈ A(p
J
k
)
for k ∈ {1, 2}.
Joining decision profile b
E
and the corresponding sets of users on the two platforms, J
E
1
and
J
E
2
, constitute a pure strategy joining equilibrium if no user has a profitable deviation. That is, for
all i ∈ V,
u
i
(J
E
b
i
, a
J
E
b
i
,E
, p
J
E
b
i
,E
) ≥ u
i
(J
E
k
∪ {i}, a
J
E
k
∪{i},E
, p
J
E
k
∪{i},E
) for k 6= b
i
and
u
i
(J
E
b
i
, a
J
E
b
i
,E
, p
J
E
b
i
,E
) ≥ 0, for all i ∈ J
E
b
i
.
Note that the first condition for the joining equilibrium ensures that each user prefers the plat-
form she joins to the other platform, and given our convention that J
0
= ∅, it also implies that
users not joining either platform prefer this to joining one of the two platforms. The second condi-
tion makes sure that a user joining a platform receives nonnegative payoff, since not joining either
platform guarantees zero payoff.
4.3 Equilibrium Existence and Characterization
Since our focus is on situations in which users join online platforms and share their data, we
impose that joining values are sufficiently large.
Assumption 1. For each i ∈ V, we have
1. for all J and J
0
such that i ∈ J and J ⊂ J
0
, we have c
i
(J
0
) > c
i
(J).
2. c
i
({i}) > max
i∈V
v
i
σ
2
i
.
This assumption implies that users receive greater services from a platform when there are
more users on the platform, which captures the network effects in online services and social media.
The fact that this benefit is indexed by i means that users can prefer being on the same platform
with different sets of other users. This assumption also imposes that even when there are no other
users on a platform, the value of the services provided by the platform exceed the cost of loss
of privacy. This second aspect directly yields the next lemma, which simplifies the rest of our
analysis. For the rest of this section, we impose Assumption 1 without explicitly stating it.
Lemma 4. Each user joins one of the two platforms. In other words, b
i
= 1 or 2 for all i ∈ V.
The next theorem is the direct analogue of Theorems 1 and 2 in the previous section and char-
acterizes the Stackelberg equilibrium given joining decisions.
19

Theorem 4. Consider a joining profile b with the corresponding sets of users J
1
and J
2
. Then a pure
strategy Stackelberg equilibrium exists and satisfies
U
(k)
(J
k
, a
J
k
,E
, p
J
k
,E
) ≥ U
(k)
(J
k
, a
J
k
, p
J
k
), for all p
J
k
, a
J
k
∈ A(p
J
k
), and k = 1, 2.
Moreover, for any i ∈ J
k
the equilibrium prices are
p
J
k
,E
i
= v
i
I
i
(a
J
k
,E
) − I
i
(a
i
= 0, a
J
k
,E
−i
)
. (8)
and
u
i
(J
E
k
, a
J
E
k
,E
, p
J
E
k
,E
) = −v
i
I
i
(a
i
= 0, a
J
k
,E
−i
) + c
i
(J
k
). (9)
Although a pure strategy Stackelberg equilibrium exists, a pure strategy joining equilibrium
may not. This is because of data externalities, which make users sometimes go to the platform
where less of their information will be leaked.
12
The next example illustrates this.
Example 5. Suppose that there are three users with
Σ =
4 .05 .06
.05 4 .05
.06 .05 .3
,
and values of privacy are given by
v
1
= 0.01, v
2
= 0.99, v
3
= 1.1.
Also for simplicity, in this example we take c
i
to be a constant function c for all i (meaning that
conditional on joining a platform, all users receive the same benefit). In this setting, user 3 has
the highest value for privacy, but shares her data if she is on the same platform as user 2 (this is
because her data are highly correlated with user 2’s). However, she does not share her data if she
is on the same platform as user 1.
We next list the possible pure strategy joining profiles and show that none of them can be an
equilibrium.
1. J
1
= {1, 2}, J
2
= {3}: with this joining profile, the resulting Stackelberg equilibrium involves
platform 1 buying the data of both users 1 and 2, while platform 2 does not buy user 3’s data.
In particular, from equation (8), the price of user 1’s data can be expressed as v
1
(I
1
(a
1
=
1, a
2
= 1) − I
1
(a
1
= 0, a
2
= 1)), which yields this user a payoff of −v
1
I
1
(a
1
= 0, a
2
= 1) + c
in this candidate equilibrium. This implies that user 1 has a profitable deviation, which is to
switch to platform 2. To see that this deviation is profitable, note that after this deviation, we
12
Note that even though increasing the amount of leaked information about low-value users increases social surplus,
it reduces these users’ payoff because it enables their platform to pay less for their data. This is the reason low-value
users may prefer to have less information leaked about themselves and choose a platform with fewer other low-value
users.
20

have J
1
= {2} and J
2
= {1, 3}, and the resulting Stackelberg equilibrium involves platform
1 buying user 2’s data, while platform 2 buys user 1’s data but not user 3’s data. This gives
user 1 a payoff of c, verifying that the deviation is beneficial for her.
2. J
1
= {2, 3}, J
2
= {1}: with this joining profile, the resulting Stackelberg equilibrium involves
platform 1 buying the data of both users 2 and 3, while platform 2 buys user 1’s data. With
a similar reasoning, user 2’s payoff is −v
2
I
2
(a
2
= 0, a
3
= 1) + c. But in this case user 2
has a profitable deviation. By switching to platform 2, equation (8) implies that she will
be offered a price of v
2
(I
2
(a
2
= 1, a
1
= 1) − I
2
(a
2
= 0, a
1
= 1)) and receive a payoff of
−v
2
I
1
(a
2
= 0, a
1
= 1) + c, which exceeds her candidate equilibrium payoff.
3. J
1
= {1, 3}, J
2
= {2}: in this case, with a similar reasoning, user 3 has a profitable deviation.
In the candidate equilibrium, this user receives a payoff of −v
3
I
3
(a
1
= 1, a
3
= 0) + c, and
if she deviates and switches to platform 2, she receives the greater payoff of −v
3
I
3
(a
2
=
1, a
3
= 0) + c.
4. J
1
= {1, 2, 3}, J
2
= ∅: in this case, user 3 again has a profitable deviation and can increase
her payoff from −v
3
I
3
(a
1
= 1, a
2
= 1, a
3
= 0) + c to c by switching to platform 2. This
establishes that there is no pure strategy equilibrium in this game.
Even though a pure strategy equilibrium may fail to exist, we next show that a mixed strategy
joining equilibrium always exists.
Definition 3. For any user i ∈ V, let B
i
be the set of probability measures over {1, 2} and β
i
∈ B
i
be a mixed strategy. We also let β ∈
Q
i∈V
B
i
be a mixed strategy profile. Then β
E
is a mixed
strategy joining equilibrium if
u
i
(β
E
i
, β
E
−i
, a
E
, p
E
) ≥ u
i
(β
i
, β
E
−i
, a
E
, p
E
), for all i ∈ V and β
i
∈ B
i
,
where u
i
(β
i
, β
−i
, a
E
, p
E
) = E
b
i
∼β
i
,b
−i
∼q
−i
u
i
(b
i
, b
−i
, a
E
, p
E
)
.
Theorem 5. There always exists a mixed strategy joining equilibrium in which all users join each platform
with probability 1/2.
Theorem 5 follows since when all other users are choosing one of the two platforms uniformly
at random (each with probability 1/2), each user is indifferent between the two platforms and can
thus randomize with probability 1/2 herself.
We also note that when the benefit from joining a more crowded platform is sufficiently greater
than the benefit from joining a smaller platform, this may restore the existence of a pure strategy
equilibrium.
13
13
In Appendix B, we also prove that if all users are low-value, then the setup with competing platforms is a potential
game and thus a pure strategy equilibrium exists. Moreover, we show that the social surplus of this equilibrium is
always less than the social surplus under monopoly, because competition between the platforms leads to an inefficiently
fragmented distribution of low-value users as they try to avoid information about them being leaked by other low-value
users.
21
4.4 Inefficiency
The social surplus of strategy profile (β, a, p) is defined analogously to the equilibrium (social)
surplus in the previous section as
Social surplus(β, a) = E
b∼β
X
i∈J
1
(1 − v
i
)I
i
(a
J
1
)) + c
i
(J
1
)
+
X
i∈J
2
(1 − v
i
)I
i
(a
J
2
)) + c
i
(J
2
)
,
where the sets J
1
and J
2
are defined based on random variable b ∼ β.
A natural conjecture is that competition might redress some of the inefficiencies of data mar-
kets identified so far, either by increasing data prices or by allowing high-value users to go to a
platform where less of their information will be leaked. The next example illustrates that this is
not necessarily the case and competition may increase or reduce equilibrium surplus.
Example 6. Consider a setting with V = {1, 2}, σ
2
1
= σ
2
2
= 1, Σ
12
> 0, and v
1
< 1, and take c
i
to
be a constant function c for all i.
• Competition improves equilibrium surplus: Suppose that v
2
> 1 is sufficiently large that in equi-
librium user 2 never shares her data. Under monopoly, equilibrium data sharing decisions
are a
E
1
= 1 and a
E
2
= 0 with prices given in Theorem 2. The equilibrium surplus is
(1 − v
1
)I
1
(a
1
= 1, a
2
= 0) + (1 − v
2
)I
2
(a
1
= 1, a
2
= 0) + 2c.
With competition, equilibrium joining decisions are b
E
1
= 1, b
E
2
= 2 and equilibrium data
sharing decisions are a
J
1
,E
1
= 1 and a
J
2
,E
2
= 0 with prices given in equation (8). The equilib-
rium surplus is therefore
(1 − v
1
)I
1
(a
1
= 1, a
2
= 0) + 2c,
which is strictly greater than the equilibrium surplus under monopoly.
• Competition reduces equilibrium surplus: Suppose that v
2
< 1. Under monopoly, we have
a
E
1
= 1 and a
E
2
= 1 with prices given in Theorem 2. The equilibrium surplus is
(1 − v
1
)I
1
(a
1
= 1, a
2
= 1) + (1 − v
2
)I
2
(a
1
= 1, a
2
= 1) + 2c.
With competition, the equilibrium involves b
E
1
= 1, b
E
2
= 2, a
J
1
,E
1
= 1 and a
J
2
,E
2
= 1 with
prices given in equation (8). The equilibrium surplus is
(1 − v
1
)I
1
(a
1
= 1, a
2
= 0) + (1 − v
2
)I
2
(a
1
= 0, a
2
= 1) + 2c,
which is strictly less than the surplus under monopoly.
The next theorem, which is the analogue of Theorem 3, characterizes the conditions for effi-
ciency and inefficiency in this case.
22

Theorem 6. 1. Suppose every high-value user is uncorrelated with all other users. Then the equilib-
rium is efficient if and only if c
i
(V) − c
i
({i}) ≥ v
i
I
i
(V
(l)
\ {i}) for all i ∈ V
(l)
.
2. Suppose at least one high-value user is correlated (has a non-zero correlation coefficient) with a low-
value user. Then there exist
¯
v ∈ R
|V
(h)
|
and v ∈ R
|V
(l)
|
such that when v
(h)
≥
¯
v and v
(l)
≥ v the
equilibrium is inefficient.
3. Suppose every high-value user is uncorrelated with all low-value users and at least one high-value
user is correlated with another high-value user. Let
˜
V
(h)
⊆ V
(h)
be the subset of high-value users
correlated with at least one other high-value user. Then for each i ∈
˜
V
(h)
there exists ¯v
i
> 0 such that
if for any i ∈
˜
V
(h)
v
i
< ¯v
i
, the equilibrium is inefficient.
The results in this theorem are similar to those in Theorem 3 and again establish that the equi-
librium is generally inefficient. One important difference is that the condition for efficiency in
the first part has become more stringent with the addition of a restriction on direct benefits from
joining platforms with different subsets of users. This is because, in the presence of multiple plat-
forms, not all low-value users may end up joining the same platform since they may try to avoid
their information being leaked to the platform by other low-value users (recall, as noted in foot-
note 12, that information leakage about low-value users is socially beneficial but costly for them
as it reduces the prices that the platforms pay for their data). This fragmented allocation of users
across platforms is costly if there are gains from being on larger platforms.
The second part of the theorem is also slightly different from Theorem 3 and requires that low-
value users have some privacy concerns as well. This is to rule out the possibility that low- and
high-value users go to separate platforms, and such an allocation may maximize social surplus
despite the loss of direct benefits from forming a larger network on a single platform. However,
when low-value users care about their privacy, such an allocation cannot be sustained because
they will have an incentive to switch to the platform populated by high-value users where there
will be no information leaked about them and they will therefore be able to obtain higher prices
for their data.
14
The next proposition generalizes Proposition 4 and provides an upper bound on social surplus,
demonstrating that data markets may easily generate negative social surplus, even in the presence
of competition. Since our focus is on the implications of data market, we do not include the direct
benefits, the c
i
’s, from online platforms in this social surplus (since these can be enjoyed by users
even if there are no data markets), and refer to it as the “data social surplus”.
Proposition 6. Let β
E
be the uniform mixed joining strategy. Then
Data social surplus(β
E
, a
E
) ≤
X
i∈V
(l)
(1 − v
i
)I
i
(V) −
1
2
X
i∈V
(h)
(v
i
− 1)I
i
(V
(l)
).
14
We should add that for such a fragmented allocation of users across platforms to achieve efficiency, though possible,
is very difficult in general.
23

Value of privacy for high-value users: v
h
12345678910
Cross-community correlation: ρ
0.05
0.1
0.15
0.2
Figure 4: Shaded area shows the pairs of (ρ, v
h
) with negative equilibrium surplus in the setting
of Example 7.
Therefore, Proposition 6 implies that if
X
i∈V
(h)
(v
i
− 1)I
i
(V
(l)
) ≥ 2
X
i∈V
(l)
(1 − v
i
)I
i
(V),
then shutting down the market for data (while continuing to operate the other services on the
online platforms) is beneficial.
Note also that compared to Proposition 4, there is a 1/2 in front of the second term in data
social surplus. This reflects the fact that in the mixed strategy joining equilibrium, the set of low-
value users who will be on the same platform as a high-value user is random (and will typically be
less than the entire set of low-values users). Using the submodularity of leaked information, we
show that the expected leakage of user i’s information from the data sharing of low-value users is
greater than 1/2 times the total leaked information about this user when all low-value users are
on the same platform and share their data.
The following example provides a more explicit illustration of the results in Proposition 6.
Example 7. We consider the same setting as Example 4 but with two competing platforms. Figure
4 shows the combinations of v
h
and ρ for which the data social surplus is negative. As highlighted
in Proposition 6, when the value of privacy for high-value users is high and/or when the correla-
tion between high-value and low-value users is large, the data social surplus is negative.
4.5 Between-Platform Externalities
In this subsection, we generalize our model to allow for between-platform externalities. This
captures the fact that some of the loss of privacy may occur for people who are not on the platform,
but whose information is revealed to the platform by others’ data sharing.
To model this possibility, we now generalize the payoff of users who join platform k ∈ {1, 2}
24
to
u
i
(J
k
, a
i
, a
J
k
−i
, p
J
k
) =
p
J
k
i
− v
i
I
i
a
i
= 1, a
J
k
−i
− v
i
αI
i
a
J
k
0
+ c
i
(J
k
), a
i
= 1, k
0
6= k
−v
i
I
i
a
i
= 0, a
J
k
−i
− v
i
αI
i
a
J
k
0
+ c
i
(J
k
) a
i
= 0, k
0
6= k,
where the term αI
i
a
J
k
0
is leaked information about user i on the platform she has not joined,
and the payoff of users who have not joined either of the platforms is
−v
i
αI
i
a
J
1
− v
i
αI
i
a
J
2
.
In this specification α ∈ [0, 1] captures between-platform externalities. When α = 0, we obtain the
model studied so far in this section. When α = 1, information revealed about an individual who
is not on the platform creates the same loss of privacy.
In addition, we assume that platforms also benefit in the same manner from information leaked
about individuals who are not their current users, so the payoff of platform k ∈ {1, 2} is now
U
(k)
(J
k
, a
J
k
, p
J
k
) =
X
i∈J
k
I
i
(a
J
k
) + α
X
i∈J
k
0
I
i
(a
J
k
) −
X
i∈J
k
: a
J
k
i
=1
p
i
, k
0
6= k, (10)
where
P
i∈J
k
0
I
i
(a
J
k
) is leaked information about users on the other platform.
We next show that our main results generalize to this case. For brevity, equilibrium existence
and characterization are provided in Theorem B-1 in Appendix B, which also shows that the equi-
librium price vectors are the same as in equation (8) in Theorem 4 (because information leaked
about a user on the other platform is unaffected by her data sharing decision).
Theorem 7. 1. Suppose that every high-value user is uncorrelated with all other users. Then there
exists ¯α such that for α ≤ ¯α the equilibrium is efficient if and only if c
i
(V) − c
i
({i}) ≥ (1 −
α)I
i
(V
(l)
\ {i}) for all i ∈ V
(l)
.
2. Suppose that at least one high-value user is correlated (has a non-zero correlation coefficient) with a
low-value user. Then there exists
¯
v ∈ R
|V
(h)
|
such that for v
(h)
≥
¯
v the equilibrium is inefficient.
3. Suppose every high-value user is uncorrelated with all low-value users and at least one high-value
user is correlated with another high-value user. Let
˜
V
(h)
⊆ V
(h)
be the subset of high-value users
correlated with at least one other high-value user. Then for each i ∈
˜
V
(h)
there exists ¯v
i
> 0 such that
if for any i ∈
˜
V
(h)
v
i
< ¯v
i
, the equilibrium is inefficient.
There are a number of differences from Theorem 6. First, in addition to the conditions in the
first part of Theorem 6, we now also require the between-platform spillovers not to be too large
— otherwise, the first best may involve splitting low-value users across the two platforms. In ad-
dition, the conditions for inefficiency in the second part are slightly weaker because the between-
25

platform externalities make it more likely that the information of high-value users will be leaked
inefficiently.
Finally, the next result shows that the data social surplus can again be negative under plausible
conditions.
Proposition 7. Let β
E
be the uniform equilibrium mixed joining strategy. Then
Data social surplus(β
E
, a
E
) ≤ (1 + α)
X
i∈V
(l)
(1 − v
i
)I
i
(V) −
1 + α
2
X
i∈V
(h)
(v
i
− 1)I
i
(V
(l)
).
Proposition 7 implies that if
X
i∈V
(h)
(v
i
− 1)I
i
(V
(l)
) ≥ 2
X
i∈V
(l)
(1 − v
i
)I
i
(V),
then shutting down the market for data (while continuing to operate the other services provided
by online platforms) is once again beneficial.
4.6 Competition over Data Prices
As noted at the beginning of this section, by having users join platforms first, we have removed
the ability of online companies to set data prices in order to attract users to their platform. In this
subsection, we study this case (with no between-platform spillovers for simplicity). Existence of
equilibrium becomes more challenging in this case because of fiercer competition over data and
users, but the overall insights are similar.
The exact timing of events is as follows.
1. Platforms simultaneously offer price vectors p
1
∈ R
n
and p
2
∈ R
n
.
2. Users simultaneously decide which platform, if any, to join, i.e., b ={b
i
}
i∈V
(which deter-
mines J
1
and J
2
) and whether to share their data.
The payoffs of users and platforms are the same as before. In particular, the payoff of user
i ∈ V who joins platform b
i
∈ {1, 2} is
u
i
(a
i
, b
i
, a
−i
, b
−i
, p
1
, p
2
) =
p
b
i
i
− v
i
I
i
(a
J
b
i
) + c
i
(J
b
i
), a
i
= 1,
−v
i
I
i
(a
J
b
i
) + c
i
(J
b
i
), a
i
= 0,
where recall that a
J
k
denotes the vector of sharing decisions in the set J
k
for k = 1, 2. Assumption
1 ensures that every user joins one of the platforms. The payoff of platform k ∈ {1, 2} is
U
(k)
(p
1
, p
2
, a, b) =
X
i : b
i
=k
I
i
(a
J
k
) −
X
i : b
i
=k,a
J
k
i
=1
p
1
i
.
26

Definition 4. For given price vectors p
1
∈ R
n
and p
2
∈ R
n
, the joining and sharing profiles b and
a constitute a user equilibrium if for any i ∈ V, we have
(a
i
, b
i
) ∈ argmax
a,b
u
i
(a, b, a
−i
, b
−i
, p
1
, p
2
).
Let A(p
1
, p
2
) denote the set of user equilibria for given price vectors p
1
and p
2
. Price vectors p
1,E
,
p
2,E
, joining profile b
E
, and sharing profile a
E
constitute a pure strategy equilibrium if (a
E
, b
E
) ∈
A(p
1,E
, p
2,E
) and for any p, there exists (a, b) ∈ A(p, p
2,E
) such that
U
(1)
(p
1,E
, p
2,E
, a
E
, b
E
) ≥ U
(1)
(p, p
2,E
, a, b),
and there exists (a
0
, b
0
) ∈ A(p
1,E
, p) such that
U
(2)
(p
1,E
, p
2,E
, a
E
, b
E
) ≥ U
(2)
(p
1,E
, p, a
0
, b
0
).
We next define a mixed strategy equilibrium similarly to before, except that these strategies
will define probability distributions over price vectors for the platforms and user actions.
15
Definition 5. Let P be the set of probability measures over R
n
+
. For any user i ∈ V, let A
i
be the set
of probability measures over {0, 1} and B
i
be the set of probability measures over {1, 2}. For given
price vectors p
1
∈ R
n
and p
2
∈ R
n
, the joining and sharing profiles β ∈
Q
i∈V
B
i
and α ∈
Q
i∈V
A
i
constitute a mixed user equilibrium if for any i ∈ V, we have
u
i
(α
i
, β
i
, α
−i
, β
−i
, p
1
, p
2
) ≥ u
i
(α
0
i
, β
0
i
, α
−i
, β
−i
, p
1
, p
2
), for all α
0
i
∈ A
i
and β
0
i
∈ B
i
,
where u
i
(α
i
, β
i
, α
−i
, β
−i
, p
1
, p
2
) = E
a
i
∼α
i
,a
−i
∼α
−i
,b
i
∼β
i
,b
−i
∼β
−i
u
i
(a
i
, b
i
, a
−i
, b
−i
, p
1
, p
2
)
. We let
A(π
1
, π
2
) denote the set of mixed strategy user equilibria for given price strategies π
1
and π
2
.
Strategy price profiles π
k,E
∈ P, k = 1, 2, joining profile β
E
, and sharing profile α
E
constitute a
mixed strategy equilibrium if (α
E
, β
E
) ∈ A(π
1,E
, π
2,E
) and for any π ∈ P there exists (α, β) ∈
A(π, π
2,E
) such that
E
p
1
∼π
1,E
,p
2
∼π
2,E
,a∼α
E
,b∼β
E
h
U
(1)
(p
1
, p
2
, a, b)
i
≥ E
p
1
∼π,p
2
∼π
2,E
,a∼α,b∼β
h
U
(1)
(p
1
, p
2
, a, b)
i
,
and there exists (α
0
, β
0
) ∈ A(π
1,E
, π) such that
E
p
1
∼π
1,E
,p
2
∼π
2,E
,a∼α
E
,b∼β
E
h
U
(2)
(p
1
, p
2
, a, b)
i
≥ E
p
1
∼π
1,E
,p
2
∼π,a∼α
0
,b∼β
0
h
U
(2)
(p
1
, p
2
, a, b)
i
.
15
Note that in the models analyzed so far, after the platform (or platforms) set data prices, users no longer had the
option of switching to another platform, and we focused on the Stackelberg equilibrium where the platform set prices
anticipating user choices and selected the most advantageous user equilibrium for itself (when there were multiple
user equilibria). This meant that an equilibrium data price ensured a (weakly) greater payoff for the platform than any
other price for any other user equilibrium. Because users now make their joining decisions after price offers, we use
the standard Nash equilibrium notion and require that for each platform and any other price than its equilibrium price
there exists a user equilibrium in which the platform’s payoff is no greater than its equilibrium payoff.
27

Theorem B-2 in Appendix B establishes the existence of a mixed strategy equilibrium in this
case. Here, we characterize the more pervasive inefficiencies with this type of price competition.
We next show that the equilibrium is even more likely to be inefficient when platforms com-
pete using data prices. In particular, in contrast to the settings studied so far, the equilibrium is
inefficient not only when high-value users are correlated with other users, but also when there is
correlation only among low-value users. For this theorem, let us define:
δ = min
i,T ⊂V
c
i
(V) − c
i
(T ) and ∆ = max
i,T ⊆V
c
i
(V) − c
i
(T ).
Theorem 8. 1. Suppose every user is uncorrelated with all other users. Then the equilibrium is efficient.
2. Suppose that every high-value user is uncorrelated with all other users, but at least two low-value
users are correlated with each other. Then there exist δ,
¯
∆,
˜
∆,
¯
v, and
˜
v such that:
2-1) If δ ≥ δ, the equilibrium is efficient.
2-2) If ∆ ≤
¯
∆ and v
(l)
≤
¯
v, the equilibrium is efficient.
2-3) If ∆ ≤
˜
∆ and v
(l)
≥
˜
v, the equilibrium is inefficient.
3. Suppose that at least one high-value user is correlated with a low-value user. Then there exist
˜
δ >
¯
∆ >
¯
δ > 0,
¯
v ∈ R
|V
(h)
|
, and v ∈ R
|V
(l)
|
such that:
3-1) If v
(h)
≥
¯
v, v
(l)
≥ v, ∆ ≤
¯
∆, and δ ≥
¯
δ, the equilibrium is inefficient.
3-2) If δ ≥
˜
δ, the equilibrium is efficient.
The first part is straightforward: without correlation there is no data externality, ensuring
efficiency.
The second part is new relative to our previous results: now the equilibrium is inefficient even
when high-value users are uncorrelated with all other users. This inefficiency is caused by com-
petition using data prices. Since there is no correlation between high-value and low-value users,
the first best involves all low-value users sharing their data and all (high-value and low-value)
users joining the same platform in order to benefit from the highest joining values. However, we
show in part 2.3 that such an allocation is not an equilibrium, because the other platform can at-
tract some of the low-value users who can benefit by having less of their information leaked by
other low-value users (even though information leakage about these users is socially beneficial,
it is privately costly for them). This leads to a fragmented distribution of users across platforms,
leading to inefficiency. Parts 2.1 and 2.2 provide conditions for efficiency in terms of the c function
being sufficiently steep or the privacy concerns of low-value users being sufficiently weak.
Part 3.1 of the theorem is similar to our other inefficiency results. In this case, in the first
best all users join the same platform (because the c function is sufficiently steep), but only low-
value users uncorrelated with high-value users share their data (because v
(h)
is sufficiently high).
We show, however, that this allocation cannot be an equilibrium because the other platform can
28
deviate and attract a subset of low-value users and induce them to share their data. In part 3.2
the first best is, once again, for all users to join one of platforms. But now because the joining
values are even steeper, the other platform can no longer attract a subset of these users, while the
threat of all users switching to this other platform supports the first-best allocation (though there
also exist inefficient equilibria in this case). Finally, we show in the working paper version that
when high-value users are uncorrelated with low-value users but correlated among themselves,
the equilibrium may or may not be efficient.
5 Unknown Valuations
Our analysis has so far assumed that platforms know the value of privacy of different users. In
this section, we adopt the more realistic assumption that they do not know the exact valuations
of users, but understand that the value of privacy of user i, v
i
, has a distribution represented by
the cumulative distribution function F
i
and density function f
i
(with upper support denoted by
v
max
). Users know their own value of privacy. For simplicity, we focus on the case of a monopoly
platform and show how the platform can design a mechanism to elicit this information (in the
form of users reporting their value of privacy). We then show that all of the main insights from
our analysis generalize to this case.
We first characterize the “second best” which takes into account that the value of privacy of
each user is their private information, and then show that the second best coincides with the first
best.
Proposition 8. Let v be the reported vector of values of privacy. Then the pricing scheme
p
i
(v) =
I
i
(a(v)) +
X
j6=i
(1 − v
j
)I
j
(a(v))
− min
a∈{0,1}
n
I
i
(a) +
X
j6=i
(1 − v
j
)I
j
(a)
,
where a(v) = argmax
a∈{0,1}
n
P
i∈V
(1 − v
i
)I
i
(a) incentivizes users to report their value of privacy truth-
fully, and thus the second best coincide with the first best.
This mechanism is a variation of Vickery-Clarke-Grove mechanism (Vickrey [1961], Clarke
[1971], Groves [1973]). In particular, for any i ∈ V the price offered to user i is equal to the surplus
of all other users on the platform when user i is present minus by the surplus when user i is absent.
The second term in the price p
i
(v) can be any function of the values v
−i
, and the choice specified
in Proposition 8 guarantees that the prices are nonnegative.
The next definition generalizes our notion of equilibrium to this incomplete information setup.
It is simplified by making use of the revelation principle, which enables us to focus on incentive
compatible price and action profiles.
Definition 6. An equilibrium is a pair (a
E
, p
E
) of functions of the reported valuations v =
(v
1
, . . . , v
n
) such that each user reports its true value and the expected payoff of the platform
29

is maximized. That is,
(a
E
, p
E
) = max
a:R
n
→{0,1}
n
,p:R
n
→R
n
E
v
n
X
i=1
I
i
(a(v)) −
X
i: a
i
(v)=1
p
i
(v)
p
i
(v) − v
i
I
i
(a(v)) ≥ p
i
(v
−i
, v
0
i
) − v
i
I
i
(a(v
−i
, v
0
i
)), for all v
0
i
, v, and i ∈ V.
We also impose the following standard assumption on the (reversed) hazard rate and maintain
it throughout this section without explicitly mentioning it.
Assumption 2. For all i ∈ V, the function Φ
i
(v) = v +
F
i
(v)
f
i
(v)
is nondecreasing.
Here Φ
i
(v) is the well-known “virtual value” in incomplete information models, representing
the additional rent that the agent will capture in incentive-compatible mechanisms. In our setting,
it will enable users to obtain more of the surplus the platform infers from their data.
A sufficient condition for Assumption 2 to hold is for the reversed hazard rate f
i
(x)/F
i
(x) to
be nonincreasing. This requirement is satisfied for a variety of distributions such as uniform and
exponential (see e.g., Burkschat and Torrado [2014]).
Theorem 9. For any reported vector of values v, the equilibrium is given by
a
E
(v) = argmax
a∈{0,1}
n
n
X
i=1
(1 − Φ
i
(v
i
))I
i
(a) + Φ
i
(v
i
)I
i
(a
−i
, a
i
= 0),
and
p
E
i
(v
i
) =
Z
v
max
v
I
i
(a
E
(x, v
−i
)) − I
i
(a
E
−i
(x, v
−i
), a
i
= 0)
dx
+ v
i
I
i
(a
E
(v
i
, v
−i
)) − I
i
(a
E
−i
(v
i
, v
−i
), a
i
= 0)
.
Moreover, all users report truthfully and thus the expected payoff of the platform is
E
v
"
max
a∈{0,1}
n
n
X
i=1
(1 − Φ
i
(v
i
))I
i
(a) + Φ
i
(v
i
)I
i
(a
−i
, a
i
= 0)
#
.
We next establish that the equilibrium is inefficient under fairly plausible conditions in this
incomplete information setting as well. The main difference from our analysis so far is that an-
other relevant set is the subset of low-value users with virtual value of privacy less than one, i.e.,
Φ
i
(v
i
) ≤ 1. For the next theorem, we use the notation V
(l)
Φ
= {i ∈ V : Φ
i
(v
i
) ≤ 1} to denote this set
of users.
Theorem 10. 1. Suppose high-value users are uncorrelated with all other users and V
(l)
= V
(l)
Φ
. Then
the equilibrium is efficient.
2. Suppose some high-value users (those in V
(h)
) are correlated with users in V
(l)
Φ
. Then there exists
¯
v ∈ R
|V
(h)
|
such that for v
(h)
≥
¯
v the equilibrium is inefficient.
30
3. Suppose every high-value user is uncorrelated with all users in V
(l)
Φ
, but users in a nonempty subset
ˆ
V
(l)
of V
(l)
\ V
(l)
Φ
are correlated with at least one high-value user. Then there exist
¯
v and ˜v such that
if v
(h)
≥
¯
v and v
i
< ˜v for some i ∈
ˆ
V
(l)
, the equilibrium is inefficient.
4. Suppose every high-value user is uncorrelated with all low-value users and at least one high-value
user is correlated with another high-value user. Let
˜
V
(h)
⊆ V
(h)
be the subset of high-value users
correlated with at least one other high-value user. Then for each i ∈
˜
V
(h)
there exists ¯v
i
> 0 such that
if for any i ∈
˜
V
(h)
v
i
< ¯v
i
, the equilibrium is inefficient.
The inefficiency results in this theorem again have clear parallels to those in Theorem 3, but
with some notable differences. First, efficiency now requires all low-value users to also have vir-
tual valuations that are less than one, since otherwise user incentive compatibility constraints pre-
vent the efficient allocation. Second, the conditions for inefficiency are slightly different depending
on whether high-value users are correlated with low-value users whose virtual valuations are less
than one or greater than one.
Finally, we present the analogue of Proposition 4 in this setting. First, note that for a given
vector of user values v a similar argument to that of Lemma 3 shows that a user i with Φ
i
(v
i
) ≤ 1
will share her data in equilibrium. Using this observation, we can establish the next proposition.
Proposition 9. Consider a setting with unknown valuations. For a given v, we have
Social surplus(a
E
) ≤
X
i : v
i
∈V
(l)
(1 − v
i
)I
i
(V) −
X
i : v
i
∈V
(h)
(v
i
− 1)I
i
(V
(l)
Φ
).
Proposition 9 is similar to Proposition 4 and provides a sufficient condition for equilibrium
surplus to be negative. The only difference is that the lower bound on the negative (second) term
is evaluated for information leaked by users in V
(l)
Φ
(rather than those in V
(l)
). This is because, with
incomplete information, the platform has to compensate users according to their virtual value of
privacy and may find it too expensive to purchase the data of low-value users with Φ
i
(v
i
) > 1.
Indeed, because Φ
i
(v
i
) ≥ v
i
, we have V
(l)
Φ
⊆ V
(l)
, and thus, given v, if equilibrium surplus with
unknown valuations is negative (
P
i∈V
(h)
(v
i
− 1)I
i
(V
(l)
Φ
) >
P
i∈V
(l)
(1 − v
i
)I
i
(V)), then equilibrium
surplus with known valuations (as given in Proposition 4) is also negative.
6 Regulation
The inefficiencies documented so far raise the question of whether certain types of government
policies or regulations could help data markets function better. We briefly address this question in
this section. We first discuss taxes and then turn to a regulation scheme based on “de-correlation”
to reduce the informativeness of the data of users about others. For simplicity, we focus on the
case of a single platform with complete information.
31
6.1 Taxation
The next proposition shows that a simple Pigovian tax scheme, using personalized taxes on data
transactions, can restore the first best. For this purpose we assume that the government can im-
pose a tax t
i
on user i selling her data to the platform.
Proposition 10. Let a
W
denote the first best. Then personalized taxes satisfying
t
i
>
X
j∈V
(l)
σ
2
j
+
X
j∈V
(h)
v
j
σ
2
j
for a
W
i
= 0
t
i
= 0 for a
W
i
= 1,
implements the first-best action profile a
W
as the unique equilibrium.
The idea of the proposition is straightforward. We first prove that not taxing users who should
be sharing in the first best is sufficient to ensure that they share in the post-tax equilibrium as well
regardless of the sharing decisions of the rest of the users. Then imposing prohibitive taxes on the
data transactions of users who should not be sharing implements the first best.
Proposition 10 characterizes a set of Pigovian taxes implementing the first best, but these taxes
vary across individuals, which presupposes a huge amount of information on the part of the plan-
ner/tax authority. A natural question is whether a uniform tax scheme can also improve over the
equilibrium allocation. If equilibrium surplus is negative, then a uniform and sufficiently high tax
on data transactions can shut down the data market and improves equilibrium surplus. The next
example, however, shows that, beyond this simple case with negative equilibrium surplus, there
is no guarantee that uniform taxes on data transactions improve welfare. This is because such
taxes may prevent beneficial data trades.
Example 8. Consider a network with three users and suppose that σ
2
i
= 1 for all i ∈ {1, 2, 3}, the
correlation between X
1
and the other two random variable is 0.4, and the correlation between X
2
and X
3
is 0. We also set v
1
= 0.1, v
2
= 0.5, and v
3
= 8. The first best is a
W
= (0, 1, 0). If the uniform
tax is t ≤ 0.25, the equilibrium is a
E
= (1, 1, 0) whose surplus is 0.0625. For 0.25 < t < 0.61, the
equilibrium is a
E
= (1, 0, 0), with social surplus −0.15. Finally, for t ≥ 0.61, the equilibrium is
a
E
= (0, 0, 0) with surplus 0. Therefore, no uniform taxation scheme can improve equilibrium
surplus in this game.
Intuitively, when the tax is small, user 1 continues to share her data. When the tax rate takes
intermediate value, now both users 1 and 2 share, and this leaks considerable information about
user 3. With very high taxes, nobody shares their data. In none of these cases can we implement
the allocation where only user 2 shares.
6.2 Mediated Data Sharing and De-correlation
In this subsection, we propose a different approach to improving the efficiency of data markets.
Our analysis has clarified that a main source of inefficiency in such markets are the data external-
32

ities created by the correlation between the information/types of different users. Our approach
is based on the observation that it is possible to transform the data of different users in such a
manner as to remove the correlation that is at the root of these data externalities. We refer to such
a scheme as de-correlation.
Suppose that instead of sharing their data with the platform, users share their data with a
(trusted third-party) mediator, who can either not share these data with the platform (as in-
structed) or transform them before revealing them to the platform.
16
Recall that user i’s data
are represented by S
i
= X
i
+ Z
i
. The main idea is that the mediator collects all the data from the
users and then computes transformed variables for each user removing the correlation with the
information of other users and only shares the transformed data of those who are willing to sell
their data (but utilizes the data of others for removing the correlation with their information).
17
Formally, we consider the following de-correlation scheme:
˜
S = Σ
−1
S where S = (S
1
, . . . , S
n
)
is the vector of data of all users. Clearly,
˜
S is jointly normal and has the property that if user i does
not share her data, then the data of other users leak no information about user i’s type. This is
formally stated in the next lemma.
Lemma 5. With de-correlation, for any action profile a ∈ {0, 1}
n
, the leaked information about user i is
e
I
i
(a) = σ
2
i
− min
ˆx
i
E
X
i
− ˆx
i
˜
S
a
2
=
0, a
i
= 0,
I
i
(a
i
, a
−i
), a
i
= 1.
This lemma clarifies our claim in the Introduction and shows that the de-correlation scheme
leaves information leaked about the user sharing her data the same, but removes the leakage about
users who are not sharing their data.
We next characterize the equilibrium pricing, denoted by
˜
p
E
, and sharing profile, denoted by
˜
a
E
, with this transformation, and show that, with de-correlation, there is no information leakage
about those who do not share, and therefore they do not contribute to the platform’s payoff. More-
over, the price offered to users who share must make them indifferent between sharing and not
sharing and thus give them zero payoff (which they can guarantee by not sharing). Given this
characterization, it follows that de-correlation always improves equilibrium surplus and, more-
over, eliminates cases where the social surplus is negative.
Theorem 11. 1. The equilibrium sharing profile after de-correlation is given by
˜
a
E
= argmax
a∈{0,1}
n
X
i∈V
(1 − v
i
)
e
I
i
(a),
with prices ˜p
E
i
= v
i
e
I
i
(
˜
a
E
) for any i ∈ V such that ˜a
E
i
= 1.
16
Obviously, such a scheme can only work if the mediator is fully reliable and trusted, and this is an important
constraint in practice, which we are ignoring in this paper.
17
In practice, it may be more relevant to remove the correlation between a user’s data and the average data of different
user types. In that case, we can partition the set of users into K cells and apply this de-correlation procedure to the
average data of cells.
33

2. Let (
˜
a
E
,
˜
p
E
) and (a
E
, p
E
) denote the equilibrium with and without the de-correlation scheme, respec-
tively. Then
Social surplus(
˜
a
E
) ≥ max
Social surplus(a
E
), 0
.
That equilibrium surplus increases after de-correlation is a consequence of the fact that in the
original equilibrium the contribution of high-value users (who do not share) to social surplus is
less than or equal to zero, while after de-correlation their contribution to social surplus is greater
than or equal to zero.
18
Moreover, because there are no users with negative contribution to social
surplus after de-correlation, equilibrium surplus is always positive. This observation also implies
that the de-correlation scheme outperforms policies that shut down data markets — since instead
of achieving zero equilibrium surplus by shutting down these markets, e.g., as in Proposition 4,
this scheme always guarantees positive social surplus.
Open questions include whether such de-correlation schemes are excessively complex to be
implemented in practice and how non-mediated information sharing between platforms and users
can be prevented (since otherwise platforms can partially undo the de-correlation implemented
by the mediator).
7 Conclusion
Because data generated by economic agents are useful for solving economic, social, or technical
problems facing others in society and for designing or inventing new products and services, much
of economic analysis in this area argues that the market may produce too little data. This paper
develops the perspective that, in the presence of privacy concerns of some agents, the market may
generate too much data. Moreover, because the data of a subset of users reveal information about
other users, the market price of data tends to be depressed, creating the impression that users do
not value their privacy much. The depressed market price of data and excessive data generation
are intimately linked.
We exposit these ideas in a simple model in which a platform wishes to estimate the types of
a collection of users, and each user has personal data (based on their preferences, past behavior,
and contacts) which are correlated both with their type and with the data and types of other users.
As a result, when a user decides to share her data with the platform, this enables the platform to
improve its estimate of other users’ types. We model the market for data by allowing the platform
to offer prices (or other services) in exchange of data.
We prove the existence of an equilibrium in the data market and show that there will be too
much data shared on the platform and the price of data will be excessively depressed. The result
that the platform acquires too much data is a direct consequence of the externalities from the data
of others. The root cause of depressed data prices is the submodularity of leaked information:
18
As with personalized taxes, de-correlation involves a considerable amount of information being pooled in the
hands of a centralized body. The difference, however, is that de-correlation, by ensuring that no information is leaked
about users who do not want to share their data, makes such information pooling incentive compatible. Providing
information to regulatory authorities is typically not incentive compatible.
34
when data sharing by other users already compromises the information of an individual, she has
less incentive to protect her data and privacy. We further show that under some simple condi-
tions the social surplus generated by data markets is negative, meaning that shutting down data
markets improves (utilitarian) social welfare.
We extend these results to a setting with multiple platforms. Various different types of com-
petition between platforms do not alter the fundamental forces leading to too much data sharing
and excessively low prices of data. In fact, competition may make inefficiencies worse. This is in
part because more data may be shared in the presence of competition, and also because the desire
of some users to avoid excessive data sharing about them may lead to an inefficiently fragmented
distribution of users across platforms, even when network externalities would be better exploited
by having all users join the same platform. We also extend these results to a setting in which the
value of privacy of different users are their private information.
Excessive data sharing may call for policy interventions to correct for the externalities and
the excessively low prices of data. Individual-specific (Pigovian) taxes on data transactions can
restore the first best. More interestingly, we propose a scheme based on mediated-data sharing that
can improve welfare. In particular, in our baseline model, when equilibrium surplus is negative,
shutting down data markets, for example with high uniform taxes on all data transactions, would
improve welfare. But this prevents the sharing of the data of users with low value of privacy or
high benefits from goods and services that depend on the platform accessing their data. We show
that if user data are first shared with a mediator which transforms them before revealing them
to the platform, the correlation of the data with the information of privacy-conscious users can
be eliminated, and this would improve welfare relative to the option of shutting off data markets
altogether.
We view our work as part of an emerging literature on data markets and the economics of
privacy. Several interesting areas of research are suggested by our results. First, it is important
to develop models of the marketplace for data that allow for richer types of competition between
different platforms. Second, our modeling of privacy and the use of data by the platform has been
reduced-form. Distinguishing the uses of personal data for price discrimination, advertising, and
designing of new products and services could lead to additional novel insights. For example, it
may enable an investigation of whether applications of personal data for designing personalized
services can be unbundled from their use for intrusive marketing, price discrimination, or mis-
leading advertising. Third, we only touched upon the possibility of designing new mechanisms
for improving the functioning of data markets while reducing data externalities. Our proposed
mechanism can be simplified and made more practical, for example, by aiming to remove the cor-
relation between different user classes, as noted above, or by focusing on only some types of data.
Other mediated data sharing arrangements or completely new approaches to this problem could
be developed as well, but should take into account the possibility that third parties may not be
fully trustworthy either. Finally, our result that market prices, or current user actions for protect-
ing privacy, do not reveal the value of privacy highlights the need for careful empirical analysis
35

documenting and estimating the value of data to platforms and the value that users attach to their
privacy in the presence of data externalities.
Appendix A
In this part of the Appendix, we provide some of the proofs omitted from the text. Remaining
proofs are presented in the online Appendix B and the details of several of the examples discussed
in the text are included in the working paper version.
Proof of Proposition 1
Recall that a
W
denotes the first best. For any i ∈ V we have a
W
i
= 1 if and only if Social surplus(a
W
−i
, a
i
=
1) ≥ Social surplus(a
W
−i
, a
i
= 0). Substituting the expression for the social surplus into this equa-
tion yields
X
j∈V
(1 − v
j
)
I
j
(a
W
−i
, a
i
= 1) − I
j
(a
W
−i
, a
i
= 0)
≥ 0. (A-1)
Conditional on the data provided by other users, i.e., k 6= i for which a
W
k
= 1, (X
j
, X
i
) are jointly
normal and their covariance matrix is given by
σ
2
j
− I
j
(a
W
−i
, a
i
= 0) Cov(X
i
, X
j
| a
W
−i
, a
i
= 0)
Cov(X
i
, X
j
| a
W
−i
, a
i
= 0) 1 + σ
2
i
− I
i
(a
W
−i
, a
i
= 0)
!
.
Therefore, if in addition to users k 6= i for which a
W
k
= 1, user i also shares her data, then the
leaked information of user j becomes
I
j
(a
W
−i
, a
i
= 1) = I
j
(a
W
−i
, a
i
= 0) +
Cov(X
i
, X
j
| a
W
−i
, a
i
= 0)
2
1 + σ
2
i
− I
i
(a
W
−i
, a
i
= 0)
. (A-2)
Substituting equation (A-2) into equation (A-1) completes the proof.
Proof of Lemma 1
Part 1, Monotonicity: In order to show that leaked information is monotonically increasing in the
set of users who share, it suffices to establish that for any i, j ∈ V and a
−j
∈ {0, 1}
n−1
we have
I
i
(a
j
= 1, a
−j
) ≥ I
i
(a
j
= 0, a
−j
). We next consider the two possible cases where i = j and i 6= j
and show this inequality.
• i = j: conditional on shared data, the joint distribution of (X
i
, S
i
) is normal with covari-
ance matrix
ˆσ
2
i
ˆσ
2
i
ˆσ
2
i
1 + ˆσ
2
i
!
, where ˆσ
2
i
= E[X
2
i
| a
−j
]. We have I
i
(a
i
= 1, a
−i
) = σ
2
i
−
ˆσ
2
i
−
ˆσ
4
i
1+ˆσ
2
i
≥ σ
2
i
− ˆσ
2
i
= I
i
(a
i
= 0, a
−i
), completing the proof of this part.
36

• i 6= j: conditional on shared data, the joint distribution of (X
i
, S
j
) is normal with covariance
matrix
ˆσ
2
i
ˆ
Σ
ij
ˆ
Σ
ij
1 + ˆσ
2
j
!
, where ˆσ
2
i
= E[X
2
i
| a
−j
], ˆσ
2
j
= E[X
2
j
| a
−j
], and
ˆ
Σ
ij
= E[X
i
X
j
| a
−j
].
We have I
i
(a
j
= 1, a
−j
) = σ
2
i
−
ˆσ
2
i
−
ˆ
Σ
2
ij
1+ˆσ
2
j
≥ σ
2
i
− ˆσ
2
i
= I
i
(a
j
= 0, a
−j
), completing the
proof of the monotonicity.
Part 2, Submodularity: We first introduce some additional notation for this proof. For any pair
i, j ∈ V, a
−{i,j}
is the collection of all users’ actions except for user i and user j. To prove this part,
it suffices to establish that for any a
−{i,j}
∈ {0, 1}
n−2
, we have
I
j
(a
−{i,j}
, a
j
= 1, a
i
= 0) − I
j
(a
−{i,j}
, a
j
= 0, a
i
= 0)
≥ I
j
(a
−{i,j}
, a
j
= 1, a
i
= 1) − I
j
(a
−{i,j}
, a
j
= 0, a
i
= 1).
Conditional on a
−{i,j}
, (X
j
, S
j
, S
i
) has a normal distribution with covariance matrix
ˆσ
2
j
ˆσ
2
j
ˆ
Σ
ij
ˆσ
2
j
1 + ˆσ
2
j
ˆ
Σ
ij
ˆ
Σ
ij
ˆ
Σ
ij
1 + ˆσ
2
i
,
where ˆσ
2
i
= E[X
2
i
| a
−{i,j}
], ˆσ
2
j
= E[X
2
j
| a
−{i,j}
], and
ˆ
Σ
ij
= E[X
i
X
j
| a
−{i,j}
]. Note that in
writing this matrix, we are using the fact that the correlation between X
i
and S
j
is the same as the
correlation between S
i
and S
j
(this holds because S
i
= X
i
+ Z
i
for some independent noise Z
i
).
Based on this covariance matrix,
I
j
(a
−{i,j}
, a
j
= 1, a
i
= 0) − I
j
(a
−{i,j}
, a
j
= 0, a
i
= 0) =
σ
2
j
−
ˆσ
2
j
−
ˆσ
4
j
1 + ˆσ
2
j
!!
−
σ
2
j
− ˆσ
2
j
=
ˆσ
4
j
1 + ˆσ
2
j
. (A-3)
We also have
I
j
(a
−{i,j}
, a
j
= 1, a
i
= 1) − I
j
(a
−{i,j}
, a
j
= 0, a
i
= 1)
=
σ
2
j
−
ˆσ
2
j
− (ˆσ
2
j
,
ˆ
Σ
ij
)
1 + ˆσ
2
j
ˆ
Σ
ij
ˆ
Σ
ij
1 + ˆσ
2
i
!
−1
(ˆσ
2
j
,
ˆ
Σ
ij
)
T
−
σ
2
j
−
ˆσ
2
j
−
ˆ
Σ
2
ij
1 + ˆσ
2
i
!!
=
ˆσ
4
j
(1 + ˆσ
2
i
) +
ˆ
Σ
2
ij
(1 + ˆσ
2
j
) − 2
ˆ
Σ
2
ij
ˆσ
2
j
(1 + ˆσ
2
i
)(1 + ˆσ
2
j
) −
ˆ
Σ
2
ij
−
ˆ
Σ
2
ij
1 + ˆσ
2
i
. (A-4)
Comparing (A-3) and (A-4), the submodularity of leaked information becomes equivalent to ˆσ
4
j
(1+
37
ˆσ
2
i
) +
ˆ
Σ
2
ij
(1 + ˆσ
2
j
) ≤ 2ˆσ
2
j
(1 + ˆσ
2
j
)(1 + ˆσ
2
i
), which holds because
ˆσ
4
j
(1 + ˆσ
2
i
) +
ˆ
Σ
2
ij
(1 + ˆσ
2
j
) ≤ ˆσ
2
j
(1 + ˆσ
2
j
)(1 + ˆσ
2
i
) +
ˆ
Σ
2
ij
(1 + ˆσ
2
j
)
(a)
≤ ˆσ
2
j
(1 + ˆσ
2
j
)(1 + ˆσ
2
i
) + ˆσ
2
i
ˆσ
2
j
(1 + ˆσ
2
j
) ≤ ˆσ
2
j
(1 + ˆσ
2
j
)(1 + ˆσ
2
i
) + ˆσ
2
j
(1 + ˆσ
2
j
)(1 + ˆσ
2
i
) = 2ˆσ
2
j
(1 + ˆσ
2
j
)(1 + ˆσ
2
i
),
where (a) follows from
ˆ
Σ
2
ij
≤ ˆσ
2
i
ˆσ
2
j
.
Proof of Lemma 2
Using Lemma 1, we first establish that the game is supermodular. The rest of the proof follows
from Tarski’s fixed point theorem. Specifically, for any i ∈ V, we prove that the game has increas-
ing differences property in (a
i
, a
−i
), i.e., if a
0
−i
≥ a
−i
then we have
u
i
(a
i
= 1, a
0
−i
) − u
i
(a
i
= 0, a
0
−i
) ≥ u
i
(a
i
= 1, a
−i
) − u
i
(a
i
= 0, a
−i
).
We can write
u
i
(a
i
= 1, a
0
−i
) − u
i
(a
i
= 0, a
0
−i
) = p
i
− v
i
I
i
(a
i
= 1, a
0
−i
) − I
i
(a
i
= 0, a
0
−i
)
(a)
≥ p
i
− v
i
(I
i
(a
i
= 1, a
−i
) − I
i
(a
i
= 0, a
−i
)) = u
i
(a
i
= 1, a
−i
) − u
i
(a
i
= 0, a
−i
),
where inequality (a) follows from part 2 of Lemma 1. Now consider the mapping F : {0, 1}
n
→
{0, 1}
n
where F
i
(a) = argmax
a∈{0,1}
u
i
(a, a
−i
). Using supermodularity of the game, this mapping
is order preserving and therefore Tarski’s theorem establishes that its fixed points form a complete
lattice and therefore is non-empty and has greatest and least elements. Finally, note that each fixed
point of the mapping F is a user equilibrium and vice versa. Therefore, the set of fixed points of
the mapping F is exactly the set of user equilibria denoted by A(p).
Proof of Theorem 1
We prove that the following action profile and price vector constitute an equilibrium:
a
E
= argmax
a∈{0,1}
n
X
i∈V
(1 − v
i
)I
i
(a) + v
i
I
i
(a
−i
, a
i
= 0),
and p
E
i
= v
i
I
i
a
i
= 1, a
E
−i
− I
i
a
i
= 0, a
E
−i
, if a
E
i
= 1 and p
E
i
= 0 if a
E
i
= 0. First note that
a
E
∈ A(p
E
). This is because the payoff of user i when a
E
i
= 1 is p
E
i
− v
i
I
i
(a
E
) = −v
i
I
i
(a
E
−i
, a
i
= 0).
If user i deviates and chooses not to share, her payoff would remain unchanged. However, when
a
E
i
= 0, her payoff is −v
i
I
i
(a
E
−i
, a
i
= 0), and deviation to sharing would lead to the lower payoff
of −v
i
I
i
(a
E
−i
, a
i
= 1). Therefore, faced with the price vector offer of p
E
, the users do not have a
profitable deviation from a
E
.
We next show that for any p and a ∈ A(p), we have U (a
E
, p
E
) ≥ U(a, p). Since a is a user
38

equilibrium for the price vector p, i.e., a ∈ A(p), for all i such that a
i
= 1, we must have p
i
≥
v
i
(I
i
(a
i
= 1, a
−i
) − I
i
(a
i
= 0, a
−i
)). This is because if p
i
< v
i
(I
i
(a
i
= 1, a
−i
) − I
i
(a
i
= 0, a
−i
)),
then user i would have a profitable deviation to not share her data. Thus,
U(a, p) =
X
i∈V
I
i
(a) −
X
i∈V: a
i
=1
p
i
≤
X
i∈V
I
i
(a) −
X
i∈V: a
i
=1
v
i
(I
i
(a
i
= 1, a
−i
) − I
i
(a
i
= 0, a
−i
))
=
X
i∈V
(1 − v
i
)I
i
(a) + v
i
I
i
(a
−i
, a
i
= 0) ≤ U(a
E
, p
E
).
Proof of Theorem 2
We use the following lemmas in this proof.
Lemma A-1 (Horn and Johnson [1987] Section 0.7). • The inverse of a matrix in terms of its blocks
is
A B
C D
!
−1
=
(A − BD
−1
C)
−1
−A
−1
B(D − CA
−1
B)
−1
−D
−1
C(A − BD
−1
C)
−1
(D − CA
−1
B)
−1
.
!
• Sherman-Morrison-Woodbury formula for the inverse of rank one perturbation of matrix: Suppose
A ∈ R
n×n
is an invertible square matrix and u, v ∈ R
n
are column vectors. Then A + uv
T
is
invertible if and only if 1 + v
T
A
−1
u 6= 0. If A + uv
T
is invertible, then its inverse is
(A + uv
T
)
−1
= A
−1
−
A
−1
uv
T
A
−1
1 + v
T
A
−1
u
.
Lemma A-2 (Feller [2008]Chapter 5, Theorem 5). Suppose (X
1
, . . . , X
n
) has a normal distribution
with covariance matrix Σ. The conditional distribution of X
1
given X
2
, . . . , X
n
is normal with covariance
matrix Σ
11
− d
T
D
−1
d, where D is the matrix obtained from Σ by removing the first row and the first
column and d = (Σ
12
, . . . , Σ
1n
)
T
.
We now proceed with the proof of theorem. We first prove the existence of p
a
. Let p
a
i
=
v
i
(I
i
(a
i
= 1, a
−i
) − I
i
(a
i
= 0, a
−i
)). For any price vector p such that a ∈ A(p) we have
u
i
(a
i
= 1, a
−i
) = p
i
− v
i
I
i
(a
i
= 1, a
−i
) ≥ u
i
(a
i
= 0, a
−i
) = −v
i
I
i
(a
i
= 0, a
−i
), for all i s.t. a
i
= 1.
Rearranging this inequality leads to p
i
≥ v
i
(I
i
(a
i
= 1, a
−i
) − I
i
(a
i
= 0, a
−i
)) = p
a
i
. We next find
the price vector p
a
in terms of the matrix Σ. Let S ⊆ {1, . . . , n} be the set of users who have shared
their data. Leaked information about any user i is only a function of the correlation among users in
S and the correlation between user i and the users in S. The relevant covariance matrix for finding
leaked information about user i is given by the rows and columns of the matrix Σ corresponding
to users in S ∪ {i}. Therefore, without loss of generality, we suppose that i = 1 and all users have
shared their data and work with the entire matrix Σ. We find the equilibrium price for user 1 (the
price offered to other users can be obtained similarly). With a
1
= . . . , a
n
= 1, (X
1
, S
1
, . . . , S
n
) is
39

normally distributed with covariance matrix
σ
2
1
σ
2
1
Σ
12
. . . Σ
1n
σ
2
1
1 + σ
2
1
Σ
12
. . . Σ
1n
Σ
12
Σ
12
1 + σ
2
2
. . . Σ
2n
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Σ
1n
Σ
1n
Σ
2n
. . . 1 + σ
2
n
.
Therefore, using Lemma A-2, the conditional distribution of X
1
given s
1
, . . . , s
n
is normal with
variance σ
2
1
−(σ
2
1
, Σ
12
, . . . , Σ
1n
)(I+Σ)
−1
(σ
2
1
, Σ
12
, . . . , Σ
1n
)
T
. The best estimator of X
1
given s
1
, . . . , s
n
is its mean which leads to the following leaked information
I
1
(a
1
= 1, a
−1
) = (σ
2
1
, Σ
12
, . . . , Σ
1n
)(I + Σ)
−1
(σ
2
1
, Σ
12
, . . . , Σ
1n
)
T
. (A-5)
If user 1 deviates to a
1
= 0, then (X
1
, S
2
, . . . , S
n
) has a normal distribution with covariance
σ
2
1
Σ
12
. . . Σ
1n
Σ
12
.
.
.
.
.
.
.
.
. I + D
Σ
1n
. . .
.
.
.
,
where D is obtained from Σ by removing the first row and column. Therefore, using Lemma A-2,
the conditional distribution of X
1
given s
2
, . . . , s
n
is normal with variance σ
2
1
− (Σ
12
, . . . , Σ
1n
)(I +
D)
−1
(Σ
12
, . . . , Σ
1n
)
T
and leaked information of user 1 is
I
1
(a
1
= 0, a
−1
) = (Σ
12
, . . . , Σ
1n
)(I + D)
−1
(Σ
12
, . . . , Σ
1n
)
T
. (A-6)
Using A-5 and A-6, the price offered to user 1 must satisfy
p
a
1
v
1
= (σ
2
1
, d
T
)
T
σ
2
1
+ 1 d
T
d (I + D)
!
−1
(σ
2
1
, d
T
)−
d
T
(I + D)
−1
d, where d = (Σ
12
, . . . , Σ
1n
). We next simplify the right-hand side of the above equa-
tion. Using part 1 of Lemma A-1,
(σ
2
1
, d
T
)
T
σ
2
1
+ 1 d
T
d I + D
!
−1
(σ
2
1
, d
T
) − d
T
(I + D)
−1
d = (σ
2
1
, d
T
)
T
M(σ
2
1
, d
T
) − d
T
(I + D)
−1
d,
with
M =
(σ
2
1
+ 1) − d
T
(I + D)
−1
d
−1
−
1
σ
2
1
+1
d
T
(I + D) −
1
1+σ
2
1
dd
T
−1
−(I + D)
−1
d
(σ
2
1
+ 1) − d
T
(I + D)
−1
d
−1
(I + D) −
1
1+σ
2
1
dd
T
−1
.
40

Using part 2 of Lemma A-1, we can further simplify this equation as follows:
σ
2
1
(σ
2
1
+ 1) − d
T
(I + D)
−1
d
−1
σ
2
1
− σ
2
1
1
σ
2
1
+ 1
d
T
(I + D) −
dd
T
σ
2
1
+ 1
−1
d
− d
T
(I + D)
−1
d
(σ
2
1
+ 1) − d
T
(I + D)
−1
d
−1
σ
2
1
+ d
T
(I + D) −
1
σ
2
1
+ 1
dd
T
−1
d
− d
T
(I + D)
−1
d = σ
2
1
(σ
2
1
+ 1) − d
T
(I + D)
−1
d
−1
σ
2
1
−
σ
2
1
1
σ
1
1
+ 1
d
T
(I + D)
−1
d + σ
2
1
1
σ
1
1
+ 1
d
T
(I + D)
−1
d
σ
2
1
+1
d
T
(I + D)
−1
d
1 − d
T
(I + D)
−1
d
σ
2
1
+1
− d
T
(I + D)
−1
d
(σ
2
1
+ 1) − d
T
(I + D)
−1
d
−1
σ
2
1
+
d
T
(I + D)
−1
d +
d
T
(I + D)
−1
d
σ
2
1
+1
d
T
(I + D)
−1
d
1 − d
T
(I + D)
−1
d
σ
2
1
+1
− d
T
(I + D)
−1
d
=
σ
4
1
(σ
2
1
+ 1) − I
1
(a
1
= 0, a
−1
)
−
σ
2
1
I
1
(a
1
= 0, a
−1
)
σ
2
1
+ 1
−
σ
2
1
σ
2
1
+ 1
I
1
(a
1
= 0, a
−1
)
2
(σ
2
1
+ 1) − I
1
(a
1
= 0, a
−1
)
−
I
1
(a
1
= 0, a
−1
)σ
2
1
(σ
2
1
+ 1) − I
1
(a
1
= 0, a
−1
)
+ I
1
(a
1
= 0, a
−1
) +
I
1
(a
1
= 0, a
−1
)
2
(σ
2
1
+ 1) − I
1
(a
1
= 0, a
−1
)
− I
1
(a
1
= 0, a
−1
)
=
σ
2
1
− I
1
(a
1
= 0, a
−1
)
2
(σ
2
1
+ 1) − I
1
(a
1
= 0, a
−1
)
,
where we used I
1
(a
1
= 0, a
−1
) = d
T
(I + D)
−1
d. This also implies
I
1
(a
1
= 1, a
−1
) = I
1
(a
1
= 0, a
−1
) +
σ
2
1
− I
1
(a
1
= 0, a
−1
)
2
σ
2
1
+ 1
− I
1
(a
1
= 0, a
−1
)
.
Proof of Corollary 1
Using Theorem 2, we have p
(a
i
=1,a
−i
)
i
= v
i
(σ
2
i
−I
i
(a
i
=0,a
−i
))
2
(σ
1
i
+1)−I
i
(a
i
=0,a
−i
)
, which is increasing in σ
2
i
and de-
creasing in I
i
(a
i
= 0, a
−i
). Again, using Theorem 2, we have I
i
(a
i
= 1, a
−i
) = I
i
(a
i
= 0, a
−i
) +
(σ
2
i
−I
i
(a
i
=0,a
−i
))
2
(σ
1
i
+1)−I
i
(a
i
=0,a
−i
)
, which is increasing in both I
i
(a
i
= 0, a
−i
) and σ
2
i
.
Proof of Proposition 2
We show the proof in two steps. In the first step we show p
a
i
is decreasing in |Cov(X
i
, X
j
| a)|,
denoted by
˜
Σ
ij
for any j and in the second step we show p
a
i
is decreasing in |
˜
Σ
jk
| for any j and k.
Step 1: Without loss of generality suppose i = 1, j = 2 and the rest of the users share their data.
Note that conditional on a
−{1,2}
, (X
1
, S
1
, S
2
) has a normal distribution. Let
˜σ
2
1
˜σ
2
1
˜
Σ
12
˜σ
2
1
˜σ
2
1
+ 1
˜
Σ
12
˜
Σ
12
˜
Σ
12
˜σ
2
2
+ 1
41

denote its covariance matrix where E[X
2
1
| a
−{1,2}
] = ˜σ
2
1
, E[X
1
X
2
| a
−{1,2}
] =
˜
Σ
12
, and E[X
2
2
|
a
−{1,2}
] = ˜σ
2
2
. Using Theorem 2, the price offered to user 1 is
p
1
=
˜σ
2
1
˜
Σ
12
˜σ
2
1
+ 1
˜
Σ
12
˜
Σ
12
˜σ
2
2
+ 1
!
−1
˜σ
2
1
˜ρ
12
!
−
˜
Σ
2
12
˜σ
2
2
+ 1
!
=
˜
Σ
2
12
− ˜σ
2
1
(1 + ˜σ
2
2
)
2
(1 + ˜σ
2
2
)
(1 + ˜σ
2
2
)(1 + ˜σ
2
1
) −
˜
Σ
2
12
.
Taking derivative with respect to
˜
Σ
2
12
establishes that p
a
1
is decreasing in
˜
Σ
2
12
and therefore decreas-
ing in |
˜
Σ
12
|.
Step 2: Without loss of generality suppose i = 1, j = 2, k = 3 and the rest of the users share
their data. Again, conditional on a
−{1,2,3}
, (X
1
, S
2
, S
3
) has a normal distribution with covariance
matrix
˜σ
2
1
˜
Σ
12
˜
Σ
13
˜
Σ
12
˜σ
2
2
+ 1
˜
Σ
23
˜
Σ
13
˜
Σ
23
˜σ
2
3
+ 1
,
where E[X
2
1
| a
−{1,2,3}
] = ˜σ
2
1
, E[X
2
2
| a
−{1,2,3}
] = ˜σ
2
2
, E[X
2
3
| a
−{1,2,3}
] = ˜σ
2
3
, E[X
1
X
2
| a
−{1,2,3}
] =
˜
Σ
12
, E[X
1
X
3
| a
−{1,2,3}
] =
˜
Σ
13
, and E[X
2
X
3
| a
−{1,2,3}
] =
˜
Σ
23
. Using Theorem 2 and Corollary
1, the price offered to user 1 is increasing in I
1
(a
1
= 0, a
−1
). Therefore, in order to complete the
proof, we need to prove that I
1
(a
1
= 0, a
−1
) is increasing in |Σ
23
|. We have
I
1
(a
1
= 0, a
−1
) =
˜
Σ
12
˜
Σ
13
˜σ
2
2
+ 1
˜
Σ
23
˜
Σ
23
˜σ
2
3
+ 1
!
−1
˜
Σ
12
˜
Σ
13
!
.
Taking the derivative of I
1
(a
1
= 0, a
−1
) with respect to
˜
Σ
23
yields
−2
(1 + ˜σ
2
2
)(1 + ˜σ
2
3
) −
˜
Σ
2
23
˜
Σ
13
˜
Σ
23
−
˜
Σ
12
(1 + ˜σ
2
3
)
˜
Σ
12
˜
Σ
23
−
˜
Σ
13
(1 + ˜σ
2
2
)
.
We claim that this derivative is nonnegative for
˜
Σ
23
≥ 0 and is nonpositive for
˜
Σ
23
≤ 0, establish-
ing that leaked information is increasing in |
˜
Σ
23
|.
• Suppose
˜
Σ
23
≥ 0. The derivative of I
1
(a
1
= 0, a
−1
) with respect to
˜
Σ
23
is nonnegative if
and only if
˜
Σ
13
˜
Σ
23
−
˜
Σ
12
(1 + ˜σ
2
3
)
˜
Σ
12
˜
Σ
23
−
˜
Σ
13
(1 + ˜σ
2
2
)
≤ 0. This inequality in turn is
equivalent to
˜
Σ
12
˜
Σ
13
P
˜
Σ
12
˜
Σ
13
!
≤ 0, where
P =
−
˜
Σ
23
(1 + ˜σ
2
3
) (1 + ˜σ
2
2
)(1 + ˜σ
2
3
)
˜
Σ
2
23
−
˜
Σ
23
(1 + ˜σ
2
2
)
!
. (A-7)
The proof of this case completes by noting that the matrix P in this case is negative semi-
definite with nonpositive eigenvalues 0 and −
˜
Σ
23
(2 + ˜σ
2
2
+ ˜σ
2
3
).
42
• Suppose
˜
Σ
23
≤ 0. The derivative of I
1
(a
1
= 0, a
−1
) with respect to
˜
Σ
23
is nonpositive if
and only if
˜
Σ
13
˜
Σ
23
−
˜
Σ
12
(1 + ˜σ
2
3
)
˜
Σ
12
˜
Σ
23
−
˜
Σ
13
(1 + ˜σ
2
2
)
≥ 0. This inequality in turn is
equivalent to
˜
Σ
12
˜
Σ
13
P
˜
Σ
12
˜
Σ
13
!
≥ 0. The proof is completed by noting that the matrix
P (defined in A-7) in this case is positive semi-definite with nonnegative eigen values 0 and
−
˜
Σ
23
(2 + ˜σ
2
2
+ ˜σ
2
3
).
Proof of Proposition 3
Let i ∈ V be such that a
0
i
= a
i
= 1. Using Theorem 2, we have
p
a
i
= v
i
(I
i
(a
i
= 1, a
−i
) − I
i
(a
i
= 0, a
−i
))
(a)
≥ v
i
I
i
(a
0
i
= 1, a
0
−i
) − I
i
(a
0
i
= 0, a
0
−i
)
= p
a
0
i
,
where (a) follows from submodularity of leaked information, i.e., part 2 of Lemma 1.
Proof of Lemma 3
Suppose to obtain a contradiction that in equilibrium a
E
i
= 0 for some i ∈ V with v
i
≤ 1. We prove
that there exists a deviation which increases the platform’s payoff. In particular, the platform can
deviate and offer price p
i
= v
i
I
i
(a
i
= 1, a
E
−i
) − I
i
(a
i
= 0, a
E
−i
)
so that user i shares.
From Theorem 1, the equilibrium action profile a
E
must maximize
P
i∈V
(1−v
i
)I
i
(a)+v
i
I
i
(a
i
=
0, a
−i
). We show that (a
i
= 1, a
E
−i
) increases this objective, which yields a contradiction:
X
j∈V\{i}
I
i
(a
i
= 1, a
E
−i
) − I
i
(a
i
= 0, a
E
−i
)
−
X
j∈V: a
E
j
=1
p
(a
i
=1,a
E
−i
)
j
− p
(a
i
=0,a
E
−i
)
j
+
(1 − v
i
)I
i
(a
i
= 1, a
E
−i
) + v
i
I
i
(a
i
= 0, a
E
−i
)
− I
i
(a
i
= 0, a
E
−i
)
(a)
≥ −
X
j∈V: a
E
j
=1
p
(a
i
=1,a
E
−i
)
j
− p
(a
i
=0,a
E
−i
)
j
+
(1 − v
i
)I
i
(a
i
= 1, a
E
−i
) + v
i
I
i
(a
i
= 0, a
E
−i
)
− I
i
(a
i
= 0, a
E
−i
)
(b)
≥ (1 − v
i
)
I
i
(a
i
= 1, a
E
−i
) − I
i
(a
i
= 0, a
E
−i
)
(c)
≥ 0,
where (a) follows from monotonicity of leaked information (i.e., part 1 of Lemma 1), (b) follows
from Proposition 3, and (c) follows from the fact that v
i
≤ 1 and leaked information is monotone.
This shows that for any i such that v
i
≤ 1 we must have a
E
i
= 1.
Proof of Theorem 3
We use the following notation in this proof. For any action profile a ∈ {0, 1}
n
and any subset
T ⊆ {1, . . . , n}, we let a
T
denote a vector that include all the entries of a
i
for which i ∈ T .
43

Part 1: For a given action profile a, the social surplus can be written as
Social surplus(a) =
X
i∈V
(1 − v
i
)I
i
(a)
(a)
=
X
i∈V
(l)
(1 − v
i
)I
i
(a
V
(l)
, a
V
(h)
= 0) +
X
i∈V
(h)
(1 − v
i
)I
i
(a
i
, a
−i
= 0)
(b)
≤
X
i∈V
(l)
(1 − v
i
)I
i
(V
(l)
),
where (a) follows from the fact that the data of high-value users are not correlated with the data
of any other user, and (b) follows from the fact that for i ∈ V
(l)
, leaked information about user
i (weakly) increases in the set of users who share (from part 1 of Lemma 1) and 1 − v
i
≥ 0.
Conversely, for i ∈ V
(h)
we have 1 − v
i
< 0. This implies a
W
i
= 1 if and only if i ∈ V
(l)
.
The payoff of the platform for a given action profile a (and the corresponding equilibrium
prices to sustain it) can be written as
U(a, p
a
) =
X
i∈V
(1 − v
i
)I
i
(a) + v
i
I
i
(a
i
= 0, a
−i
)
(a)
=
X
i∈V
(l)
(1 − v
i
)I
i
(a
V
(l)
) + v
i
I
i
(a
V
(l)
\{i}
) +
X
i∈V
(h)
(1 − v
i
)I
i
(a
i
, a
−i
= 0)
(b)
≤
X
i∈V
(l)
(1 − v
i
)I
i
(a
V
(l)
) + v
i
I
i
(a
V
(l)
\{i}
)
(c)
≤
X
i∈V
(l)
(1 − v
i
)I
i
(V
(l)
) + v
i
I
i
(V
(l)
\ {i})
where (a) follows from the fact that the data of high-value users are not correlated with the data
of any other user, (b) follows from the fact that 1 − v
i
< 0 for i ∈ V
(h)
, and (c) follows from Lemma
3. Therefore, no high-value user shares in equilibrium and we have a
E
= a
W
.
Part 2: Let i ∈ V
(l)
and j ∈ V
(h)
be such that Σ
ij
> 0. Therefore, there exists δ > 0 such that
I
j
(V
(l)
) = δ > 0. We next show that for v
j
> 1 +
P
i∈V
(l)
σ
2
i
δ
the surplus of the action profile a
E
is
negative, establishing that it does not coincide with the first best. We have
Social surplus(a
E
) =
X
i∈V
(l)
(1 − v
i
)I
i
(a
E
) +
X
i∈V
(h)
(1 − v
i
)I
i
(a
E
)
(a)
≤
X
i∈V
(l)
(1 − v
i
)σ
2
i
+
X
i∈V
(h)
(1 − v
i
)I
i
(a
E
)
(b)
≤
X
i∈V
(l)
(1 − v
i
)σ
2
i
+ (1 − v
j
)I
j
(V
(l)
) ≤
X
i∈V
(l)
σ
2
i
+ (1 − v
j
)I
j
(V
(l)
)
(c)
< 0
where in (a) for low-value users we have upper bounded leaked information with its maximum;
in (b) we have removed all the negative terms in the second summation except for the one corre-
sponding to j for which we have replaced the leaked information (of equilibrium action profile)
by its minimum (using Lemma 3); and in (c) we have used v
j
> 1 +
P
i∈V
(l)
σ
2
i
δ
.
Part 3: Let i, k ∈ V
(h)
be such that Σ
ik
> 0. The first best involves all low-values are sharing their
data and none of the high-value users doing so. We next show that if the value of privacy for high-
value user i is small enough, then at least one high-value user shares in equilibrium. We show this
44

by assuming the contrary and then reaching a contradiction. Suppose that none of high-value
users share. We show that if user i shares, the platform’s payoff increases. We let a
0n
denote the
sharing profile in which all users in V
(l)
∪ {i} share their data and a ∈ {0, 1}
n
denote the sharing
profile in which all users in V
(l)
share their data. Using this notation, let us write
U(a
0
, p
a
0
) = (1 − v
i
)I
i
(V
(l)
∪ {i}) + v
i
I
i
(V
(l)
) +
X
k∈V
(h)
\{i}
I
k
(V
(l)
∪ {i})
+
X
j∈V
(l)
(1 − v
j
)I
j
(V
(l)
∪ {i}) + v
j
I
j
(V
(l)
∪ {i} \ {j})
(a)
= (1 − v
i
)I
i
(V
(l)
∪ {i}) + v
i
I
i
(V
(l)
) +
X
k∈V
(h)
\{i}
I
k
(V
(l)
∪ {i})
+ U(a, p
a
)
(b)
> U (a, p
a
),
where (a) follows from the fact that high- and low-value users are uncorrelated and (b) follows by
letting
v
i
<
I
i
(V
(l)
∪ {i}) +
P
k∈V
(h)
\{i}
I
k
(V
(l)
∪ {i})
I
i
(V
(l)
∪ {i}) − I
i
(V
(l)
)
=
I
i
({i}) +
P
k∈V
(h)
\{i}
I
k
({i})
I
i
({i})
.
Finally, note that using Σ
ik
> 0, the right-hand side of the above inequality is strictly larger than
1. The proof is completed by letting ¯v
i
=
I
i
({i})+
P
k∈V
(h)
\{i}
I
k
({i})
I
i
({i})
.
Proof of Proposition 4
For an equilibrium action profile a
E
, social surplus can be written as
Social surplus(a
E
) =
X
i∈V
(1 − v
i
)I
i
(a
E
)
(a)
≤
X
i∈V
(l)
(1 − v
i
)I
i
(V) +
X
i∈V
(h)
(1 − v
i
)I
i
(V
(l)
)
where (a) follows from the fact that for i ∈ V
(l)
, leaked information about user i increases in the
set of users who share (i.e., part 1 of Lemma 1) and 1 − v
i
≥ 0; and for i ∈ V
(h)
we have 1 − v
i
< 0
and I
i
(a
E
) ≥ I
i
(V
(l)
) by using Lemma 3.
Proof of Proposition 5
Using Theorem 2, leaked information about a high-value user i ∈ V
(h)
if low-value users share is
(Σ
ij
1
, . . . , Σ
ij
k
)((I + Σ) + M )
−1
(Σ
ij
1
, . . . , Σ
ij
k
)
T
,
where low-value users are denoted by j
1
, . . . , j
k
and the diagonal entries of M are zero and M
r,s
is
the covariance between two low-value users r and s. We next prove that this leaked information
is larger than or equal to
P
k
l=1
Σ
2
ij
l
||Σ||
1
+1
, where ||Σ||
1
= max
i=1,...,n
P
n
j=1
|Σ
ij
|. We first show that
45

((I +Σ)+M)
−1
−((||Σ||
1
+ 1)I)
−1
0 (i.e., the matrix ((I +Σ)+M)
−1
−((||Σ||
1
+ 1)I)
−1
is positive
semidefinite). Letting µ
i
denote an eigen value of the matrix ((I + Σ) + M)
−1
− ((||Σ||
1
+ 1)I)
−1
,
it suffices to show that µ
i
≥ 0. There exists an eigenvalue, λ
i
, of the matrix (I + Σ) + M for which
we have µ
i
=
1
λ
i
−
1
||Σ||
1
+1
. We next show that all eigenvalues of the matrix (I + Σ) + M are
(weakly) smaller than ||Σ||
1
+ 1, which establishes that µ
i
≥ 0. Using Gershgorin Circle Theorem,
the matrix (||Σ||
1
+ 1)I − ((I + Σ) + M) is positive semidefinite. This is because for row i of this
matrix, the diagonal entry is ||Σ||
1
− Σ
ii
which is larger than the summation of the absolute values
of the off-diagonal entries
P
j6=i
Σ
ij
. Therefore, for any eigenvalue of the matrix (I + Σ) + M such
as λ
i
, we have λ
i
≤ ||Σ||
1
+ 1. We can write
(Σ
ij
1
, . . . , Σ
ij
k
)((I + Σ) + M )
−1
(Σ
ij
1
, . . . , Σ
ij
k
)
T
≥ (Σ
ij
1
, . . . , Σ
ij
k
)((||Σ||
1
+ 1)I)
−1
(Σ
ij
1
, . . . , Σ
ij
k
)
T
=
k
X
l=1
Σ
2
ij
l
||Σ||
1
+ 1
. (A-8)
Using Proposition 4, equilibrium surplus is negative if
P
i∈V
(h)
(v
i
− 1)I
i
(V
(l)
) >
P
i∈V
(l)
(1 −
v
i
)I
i
(V). From inequality (A-8) and I
i
(V) ≤ 1, this condition holds provided that
X
i∈V
(h)
(v
i
− 1)
P
j∈V
(l)
Σ
2
ij
||Σ
(l)
|| + 1
>
X
i∈V
(l)
(1 − v
i
),
where Σ
(l)
denotes the submatrix of Σ which only includes the rows and columns corresponding
to low value users. This completes the proof.
References
A. Acquisti and H. R. Varian. Conditioning prices on purchase history. Marketing Science, 24(3):
367–381, 2005.
A. Acquisti, C. Taylor, and L. Wagman. The economics of privacy. Journal of Economic Literature,
54(2):442–92, 2016.
A. R. Admati and P. Pfleiderer. A monopolistic market for information. Journal of Economic Theory,
39(2):400–438, 1986.
A. Agarwal, M. Dahleh, and T. Sarkar. A marketplace for data: an algorithmic solution. Proceedings
of the 2019 ACM Conference on Economics and Computation, pages 701–726, 2019.
A. Agrawal, J. Gans, and A. Goldfarb. Prediction machines: the simple economics of artificial intelli-
gence. Harvard Business Press, 2018.
J. J. Anton and D. A. Yao. The sale of ideas: Strategic disclosure, property rights, and contracting.
The Review of Economic Studies, 69(3):513–531, 2002.
S. Athey, C. Catalini, and C. Tucker. The digital privacy paradox: Small money, small costs, small
talk. Technical report, National Bureau of Economic Research, 2017.
46
M. Babaioff, R. Kleinberg, and R. Paes Leme. Optimal mechanisms for selling information. In
Proceedings of the 13th ACM Conference on Electronic Commerce, pages 92–109, 2012.
J. Begenau, M. Farboodi, and L. Veldkamp. Big data in finance and the growth of large firms.
Journal of Monetary Economics, 97:71–87, 2018.
D. Bergemann and A. Bonatti. Selling cookies. American Economic Journal: Microeconomics, 7(3):
259–94, 2015.
D. Bergemann and A. Bonatti. Markets for information: An introduction. Annual Review of Eco-
nomics, 11, 2019.
D. Bergemann, A. Bonatti, and A. Smolin. The design and price of information. American Economic
Review, 108(1):1–48, 2018.
D. Bergemann, A. Bonatti, and T. Gan-a. The Economics of Social Data. Cowles Foundation Discus-
sion Paper, 2019.
M. Burkschat and N. Torrado. On the reversed hazard rate of sequential order statistics. Statistics
& Probability Letters, 85:106–113, 2014.
Y. Chen and S. Zheng. Prior-free data acquisition for accurate statistical estimation. Proceedings of
the 2019 ACM Conference on Economics and Computation, pages 659–677, 2019.
Y. Chen, N. Immorlica, B. Lucier, V. Syrgkanis, and J. Ziani. Optimal data acquisition for statistical
estimation. In Proceedings of the 2018 ACM Conference on Economics and Computation, pages 27–44,
2018.
J. P. Choi, D. S. Jeon, and B. C. Kim. Privacy and personal data collection with information exter-
nalities. Journal of Public Economics, 173:113–124, 2019.
E. H. Clarke. Multipart pricing of public goods. Public choice, 11(1):17–33, 1971.
P. Dasgupta and E. Maskin. The existence of equilibrium in discontinuous economic games, I:
Theory. Review of Economic Studies, 53(1):1–26, 1986.
T. Cover and J. Cover. Elements of Information Theory. John Wiley & Sons, 2012.
C. Dwork and A. Roth. The algorithmic foundations of differential privacy. Foundations and
Trends
R
in Theoretical Computer Science, 9(3-4):211–407, 2014.
K. Eliaz, R. Eilat and X. Mu. Optimal Privacy-Constrained Mechanisms. CEPR Discussion Paper
No. DP13536, 2019.
P. Es
˝
o and B. Szentes. Optimal information disclosure in auctions and the handicap auction. The
Review of Economic Studies, 74(3):705–731, 2007.
J. A. Fairfield and C. Engel. Privacy as a public good. Duke Law Journal, 65(3):385–457, 2015.
W. Feller. An introduction to probability theory and its applications, volume 2. John Wiley & Sons,
2008.
A. Goldfarb and C. Tucker. Online display advertising: Targeting and obtrusiveness. Marketing
Science, 30(3):389–404, 2011.
47
A. Goldfarb and C. Tucker. Shifts in privacy concerns. American Economic Review, 102(3):349–53,
2012.
A. Ghosh and A. Roth. Selling privacy at auction. Games and Economic Behavior, 91:334–346, 2015.
T. Groves. Incentives in teams. Econometrica: Journal of the Econometric Society, 41(4):617–631, 1973.
R. A. Horn and C. R. Johnson. Matrix analysis. Cambridge, Cambridge, 1987.
J. Horner and A. Skrzypacz. Selling information. Journal of Political Economy, 124(6):1515–1562,
2016.
C. I. Jones and C. Tonettil. Nonrivalry and the economics of data. In 2018 Meeting Papers, number
477. Society for Economic Dynamics, 2018.
K. C. Laudon. Markets and privacy. Communications of the ACM, 39(9):92–104, 1996.
M. MacCarthy. New directions in privacy: Disclosure, unfairness and externalities. I/S: A Journal
of Law and Policy for the Information Society, 6:425–512, 2011.
R. Montes, W. Sand-Zantman, and T. Valletti. The value of personal information in online markets
with endogenous privacy. Management Science, 65(3):1342–1362, 2018.
F. Pasquale. The black box society. Harvard University Press, 2015.
E. A. Posner and E. G. Weyl. Radical markets: Uprooting capitalism and democracy for a just society.
Princeton University Press, 2018.
R. A. Posner. The economics of privacy. The American economic review, 71(2):405–409, 1981.
G. J. Stigler. An introduction to privacy in economics and politics. The Journal of Legal Studies, 9(4):
623–644, 1980.
C. R. Taylor. Consumer privacy and the market for customer information. RAND Journal of Eco-
nomics, 35(4):631–650, 2004.
J. Tirole. Digital dystopia. 2019.
H. R. Varian. Economic aspects of personal privacy. In Internet policy and economics, pages 101–109,
2009.
L. Veldkamp. Data and the aggregate economy. 2019.
L. Veldkamp, M. Farboodi, R. Mihet, and T. Philippon. Big data and firm dynamics. 2019.
W. Vickrey. Counterspeculation, auctions, and competitive sealed tenders. The Journal of finance,
16(1):8–37, 1961.
S. D. Warren and L. D. Brandeis. The right to privacy. Harvard law review, 4(5):193–220, 1890.
A. F. Westin. Privacy and freedom. Washington and Lee Law Review, 25(1):166, 1968.
S. Zuboff. The age of surveillance capitalism: The fight for a human future at the new frontier of power.
Profile Books, 2019.
48
Appendix B: Online Appendix for “Too Much Data: Prices and Ineffi-
ciencies in Data Markets”
B.1 Proof of Pure Strategy Existence and Inefficiency When v
i
≤ 1 for all users
We show that with competition if v
i
< 1, c
i
is equal to constant c, and 1 >
P
n
j=1
|Σ
ij
| for all i ∈ V,
then a pure strategy equilibrium exists. Since all v
i
’s are below one, in the Stackelberg equilibrium
(in the second stage) all users share their data. We next show that the first stage game has a pure
strategy equilibrium. In particular, we prove the game is a potential game. Suppose the set S of
users join the first platform (and also share their data). The payoff of a user i ∈ S is
u
i
= p
i
− v
i
I
i
(S) + c = v
i
(I
i
(S) − I
i
(S \ {i})) − v
i
I
i
(S) + c = −v
i
I
i
(S \ {i}) + c.
Therefore, if in equilibrium set S of users join the first platform and the rest (i.e., the set S
c
) join
the second platform, then we must have
I
i
(S
c
) ≥ I
i
(S \ {i}), for all i ∈ S, and I
i
(S) ≥ I
i
(S
c
\ {i}), for all i ∈ S
c
.
This means that leaked information of a user on platform 1 (if she does not share) must be smaller
than her leaked information on platform 2 (if she joins that platform). That is, the information
leakage due to externality on the platform that a user joins is smaller than the other platform.
Before introducing the potential function, we introduce some additional notation. Consider a
graph with the set of nodes {1, . . . , n} and edge weights Σ
ij
(with self-loops of weights σ
2
i
). A walk
is a finite sequence of edges which joins a sequence of vertices. A closed walk is a walk in which the
first and the last vertices are the same. We define the weight of a walk as the product of the weights
of its edges. For any i ∈ V and a given set S ⊆ {1, . . . , n}, S
c
, and n
1
, n
2
∈ N we let W(i; n
1
, n
2
; S)
be the sum over the weight of all closed walks that start from node i, visits n
1
nodes in the set
S \ {i} and n
2
nodes in the set S
c
\ {i}.
We first provide a reformulation of leaked information in terms of these objects.
Claim 1: For any node i ∈ S we have
I
i
(S \ {i}) =
∞
X
t=1
(−1)
t+1
W(i; t, 0; S).
Suppose, without loss of generality, S = {1, . . . , k}. We also let Σ denote the rows and columns of
the covariance matrix corresponding to the users in the set S. Leaked information of user i 6∈ S
as characterized in Theorem 2 is (Σ
i1
, . . . , Σ
ik
)(I + Σ)
−1
(Σ
i1
, . . . , Σ
ik
)
T
. Given 1 >
P
n
j=1
|Σ
ij
|, we
have 1 >
P
j∈S
|Σ
ij
| for all i ∈ S and Gershgorin Circle Theorem shows that ρ(Σ) < 1. Therefore,
the Taylor expansion of I + Σ is convergent and we can rewrite the above expression as
(Σ
i1
, . . . , Σ
ik
)
I − Σ + Σ
2
− Σ
3
+ . . .
(Σ
i1
, . . . , Σ
ik
)
T
B-1
=
k
X
j=1
Σ
2
ij
−
X
j
1
,j
2
∈S
Σ
ij
1
Σ
j
1
j
2
Σ
j
2
i
+
X
j
1
,j
2
,j
3
∈S
Σ
ij
1
Σ
j
1
j
2
Σ
j
2
j
3
Σ
j
3
i
− · · · =
∞
X
t=1
(−1)
t+1
W(i; t, 0; S).
Claim 2: For any set S and S
c
, we have
X
n
1
,n
2
≥1
(−1)
n
1
+n
2
+1
W(i; n
1
, n
2
; S) =
X
n
1
,n
2
≥1
(−1)
n
1
+n
2
+1
W(i; n
1
, n
2
; S
c
).
This holds true because by definition of the weight of walks we have W(i; n
1
, n
2
; S) = W(i; n
2
, n
1
; S
c
).
Claim 3: The following is a potential function of the first stage game:
Ψ(S) =
X
i∈S
X
n
1
,n
2
: n
1
≥1
(−1)
n
1
+n
2
+1
W(i; n
1
, n
2
; S) +
X
i∈S
s
X
n
1
,n
2
: n
2
≥1
(−1)
n
1
+n
2
+1
W(i; n
1
, n
2
; S
c
).
Moreover, the following set S is the equilibrium of the first stage game:
S ∈ argmax
T
Ψ(T ).
First note that there are finitely many sets T (i.e., 2
n
of them) and therefore the maximizer of Ψ(·)
exists. We next prove that the maximizer of Ψ(·) corresponds to a pure strategy equilibrium of the
first stage game, i.e.,
I
i
(S
c
) ≥ I
i
(S \ {i}), for all i ∈ S, and I
i
(S) ≥ I
i
(S
c
\ {i}), for all i ∈ S
c
.
Let i ∈ S. Since S is the maximizer of Ψ(·), by moving i from S to S
c
we obtain Ψ(S \ {i}) ≤ Ψ(S).
We further have
Ψ(S \ {i})
(a)
= Ψ(S) −
X
n
1
,n
2
: n
1
≥1
(−1)
n
1
+n
2
+1
W(i; n
1
, n
2
; S) +
X
n
1
,n
2
: n
2
≥1
(−1)
n
1
+n
2
+1
W(i; n
1
, n
2
; S
c
)
(b)
= Ψ(S) −
X
n
1
≥1
(−1)
n
1
+1
W(i; n
1
, 0; S) +
X
n
2
≥1
(−1)
n
2
+1
W(i; 0, n
2
; S
c
)
(c)
= Ψ(S) − I
i
(S
c
) + I
i
(S \ {i}) ≤ Ψ(S),
where (a) follows from the fact that by moving i from S to S
c
the terms W(j; n
1
, n
2
; S) for all other
j 6= i do not change, (b) follows from Claim 2, and (c) follows from Claim 1. Therefore, we have
I
i
(S
c
) ≥ I
i
(S \ {i}). This completes the proof of Claim 2.
Using an identical argument shows that for all i ∈ S
c
, we have I
i
(S) ≥ I
i
(S
c
\ {i}). This
completes the proof of existence of a pure strategy equilibrium.
We next show that when all values are below 1, the equilibrium is always inefficient. Suppose
S and S
c
are the equilibrium joining (and sharing) sets on platforms 1 and 2, respectively. The
social surplus becomes
P
i∈S
(1 − v
i
)I
i
(S) +
P
i∈S
c
(1 − v
i
)I
i
(S
c
) ≤
P
i∈V
(1 − v
i
)I
i
(V), where the
inequality follows from the monotonicity of leaked information (Lemma 1). Note that the right-
B-2
hand side is the equilibrium surplus when we have a single platform, completing the proof.
B.2 Remaining Proofs
Proof of Lemma 4
The payoff of user i from joining platform k ∈ {1, 2} can be lower bounded by
c
i
(J
k
) + p
J
k
,E
i
− v
i
I
i
(a
J
k
,E
)
(a)
= c
i
(J
k
) − v
i
I
i
(a
J
k
,E
−i
, a
i
= 0)
(b)
≥ c
i
({i}) − v
i
σ
2
i
,
which is positive given Assumption 1. Equality (a) follows from the characterization of equilib-
rium prices given in Theorem 2, and inequality (b) follows from the monotonicity of the joining
value function c
i
(·) and the fact that maximum leaked information is σ
2
i
.
Proof of Theorem 4
After the joining decisions are made, the equilibrium characterization of the sharing profile and
the price vector on each platform is identical to that of Theorems 1 and 2.
Proof of Theorem 5
The theorem follows from the fact by using a uniform mixed strategy, the two platforms generate
the same ex ante expected payoff for users, hence no user has an incentive to deviate from uniform
randomization.
Proof of Theorem 6
Part 1: When high-value users are not correlated with other users, the first best is to have all users
join one of the platforms and to have all low-value users share. This is because: (i) the high-value
users do not share because the data of high-value users do not increase leaked information of
low-value users and generate negative surplus, (ii) the low value users share because it generates
a positive surplus itself and also increases leaked information of other low-value users (and does
not leak information about high-value users), and (iii) all users join the same platform because it
increases the joining value as well as leaked information of low-value users. We next show that
this is an equilibrium if and only if
c
i
(V) − c
i
({i}) ≥ I
i
(V
(l)
\ {i}) for all i ∈ V
(l)
. (B-1)
If inequality (B-1) holds, then the first best is an equilibrium: First, note that high-value users
do not have an incentive to deviate to the other platform because they would gain c
i
({i}) instead
of c
i
(V). Second, consider i ∈ V
(l)
and suppose she deviates and joins the other platform. Her
payoff changes from c
i
(V) − v
i
I
i
(V
(l)
\ {i}) to c
i
({i}). This is not a profitable deviation when
inequality (B-1) holds.
B-3

If inequality (B-1) does not hold, then the first best is not an equilibrium: Given inequality (B-1)
does not hold, there exists i ∈ V
(l)
such that c
i
(V)−c
i
({i}) < I
i
(V
(l)
\{i}). We let v
i
=
c
i
(V)−c
i
({i})
I
i
(V
(l)
\{i})
+
for =
1
2
1 −
c
i
(V)−c
i
({i})
I
i
(V
(l)
\{i})
, and show that all users joining the first platform and low-value users
sharing on platform 1 is not an equilibrium. With this choice for , v
i
is less than 1 and strictly
larger than
c
i
(V)−c
i
({i})
I
i
(V
(l)
\{i})
. In particular, we show that user i has a profitable deviation by joining
platform 2. Using Theorem 4, the payoff of user i on platform 1 is −v
i
I
i
(V
(l)
\ {i}) + c
i
(V). If
she deviates and joins platform 2, her payoff becomes (again using Theorem 4) c
i
({i}). This is a
profitable deviation because
− v
i
I
i
(V
(l)
\ {i}) + c
i
(V)
(a)
= −
c
i
(V) − c
i
({i})
I
i
(V
(l)
\ {i})
+
I
i
(V
(l)
\ {i}) + c
i
(V)
= − (c
i
(V) − c
i
({i})) − I
i
(V
(l)
\ {i}) + c
i
(V) = −I
i
(V
(l)
\ {i}) + c
i
({i}) < c
i
({i}).
where in (a) we substituted the value of v
i
.
Part 2: Let V
(l)
1
= {i ∈ V
(l)
: ∀j ∈ V
(h)
, Σ
ij
= 0} be the set of low-value users whose correlation
with all high-value users are zero and V
(l)
2
= V
(l)
\ V
(l)
1
be the set of low-value users with at least
one non-zero correlation coefficient to a high-value user. By assumption, there exists at least one
non-zero correlation coefficient between high and low-value users, showing V
(l)
2
6= ∅. We next
show that there exist
¯
v ∈ R
|V
(h)
|
and v ∈ R
|V
(l)
|
such that for v
(h)
≥
¯
v and v
(l)
≥ v, the first
best is to have all users joining the same platform and low-value users in V
(l)
1
share their data.
Suppose the contrary, i.e., a subset of users J
1
join the first platform and users in S
1
⊆ J
1
share
their data, and the rest of the users J
2
= V \ J
1
join the second platform and users in S
2
⊆ J
2
share
on platform 2. For large enough
¯
v on each platform, leaked information of high-value users must
be zero. Therefore, for the set of users sharing on platforms 1 and 2, we have S
1
, S
2
⊆ V
(l)
. For
sufficiently large v, the surplus is upper bounded as follows:
X
i∈J
1
(1 − v
i
)I
i
(S
1
) + c
i
(J
1
) +
X
i∈J
2
(1 − v
i
)I
i
(S
2
) + c
i
(J
2
)
(a)
≤
X
i∈V
(l)
(1 − v
i
)I
i
(V
(l)
) +
X
i∈J
1
c
i
(J
1
) +
X
i∈J
2
c
i
(J
2
)
(b)
≤
X
i∈V
(l)
(1 − v
i
)I
i
(V
(l)
1
) +
X
i∈V
c
i
(V),
where (a) follows from the fact that only low-value users have a non-zero leaked information
(because the value of high value users is large) and their leaked information is upper bounded
by their leaked information when all low-value users share, and (b) follows from the fact if all
low-value users are very close to 1, then the inequality in (b) holds because of the monotonicity of
c
i
, and therefore there exists v close enough to 1 for which (b) holds.
Now note that this cannot be an equilibrium because in equilibrium all low-value users share,
but in the first best the low-value user who has a non-zero correlation coefficient with one of the
high-value users should not be sharing (i.e., those users in V
(l)
2
6= ∅ should not be sharing).
Part 3: Let users i, k ∈ V
(h)
be such that Σ
ik
> 0. The first best is to have all users joining the same
B-4

platform, which we assume without loss of generality is platform 1, all low-value users share and
none of the high-value users share. This is because high-value users have no externality on low-
value users and therefore they should never share in the first best. They join the same platform as
low-value users to enjoy the higher joining value. Also, all low-value users join the same platform
and since they have a zero correlation coefficient with high-value users, they should all share in
the first best. An identical argument to that of Part 3 of Theorem 3 shows that for sufficiently small
value v
i
, user i shares on platform 1, establishing that the first best cannot be equilibrium.
Proof of Proposition 6
The proof is very similar to the proof of Proposition 4. In particular, similar to Lemma 3, for
any joining profile in the Stackelberg equilibrium users with values below one share. Similar to
Proposition 4, we can lower bound leaked information about high-value users such as i with their
leaked information when only low-value users shares; and upper bound the leaked information
of low-value users such as i with their leaked information when all users share. We next provide
the lower bound on the leaked information of a high-value user i:
E
β
I
i
(a
J,E
)
(a)
=
1
2
E
β
−i
I
i
(a
J
1
,E
)
+
1
2
E
β
−i
I
i
(a
J
2
,E
)
(b)
≥
1
2
E
β
−i
h
I
i
(V
(l)
∩ J
1
)
i
+
1
2
E
β
−i
h
I
i
(V
(l)
∩ J
2
)
i
= E
β
−i
1
2
I
i
(V
(l)
∩ J
1
) +
1
2
I
i
V
(l)
\
V
(l)
∩ J
1
(c)
≥ E
β
−i
1
2
I
i
(V
(l)
)
=
1
2
I
i
(V
(l)
).
where (a) follows from the fact that we have uniform mixed joining strategy, (b) follows from the
fact that on each platform all low-value users share their information, and (c) follows from the fact
that leaked information is submodular.
Proof of Theorem 7
We first state a generalization of our equilibrium existence result.
Theorem B-1. For any joining profile b with the corresponding sets of users J
1
and J
2
, there exists a pure
strategy Stackelberg equilibrium with equilibrium prices as in equation (8) and equilibrium payoffs of users
joining platform k given by
u
i
(J
E
k
, a
J
E
k
,E
, p
J
E
k
,E
) = −v
i
I
i
(a
i
= 0, a
J
k
,E
−i
) − v
i
αI
i
(a
J
k
0
,E
) + c
i
(J
k
). (B-2)
Moreover, there always exists a mixed strategy joining equilibrium in which all users join each platform
with probability 1/2.
The proof of this theorem is straightforward and is omitted. Given this existence and charac-
terization result (where the price vector is identical to that in Theorem 4), the proof of Theorem 7
follows closely that of Theorem 6, and is omitted as well.
B-5

Proof of Proposition 7
We let J
1
and J
2
be the set of users joining platforms 1 and 2, respectively and S
1
and S
2
be the
set of users sharing on platforms 1 and 2 respectively. The sum of the platform’s utilities can be
written as
X
i∈J
1
I
i
(S
1
) + αI
i
(S
2
) − p
i
+
X
i∈J
2
I
i
(S
2
) + αI
i
(S
1
) − p
i
. (B-3)
Also, the summation of users’ utilities (excluding the joining value) can be written as
X
i∈J
1
p
i
− v
i
I
i
(S
1
) − v
i
αI
i
(S
2
) +
X
i∈J
2
p
i
− v
i
I
i
(S
2
) − v
i
αI
i
(S
1
) − p
i
. (B-4)
Taking summation of equations (B-3) and (B-4), the data social surplus becomes
X
i∈J
1
(1 − v
i
)(I
i
(S
1
) + αI
i
(S
2
)) +
X
i∈J
2
(1 − v
i
)(I
i
(S
2
) + αI
i
(S
1
)).
The rest of the proof is identical to that of Proposition 6 with the only difference that for a low-
value user i ∈ V that joins platform k ∈ {1, 2}, we use the bound I
i
(a
J
k
,E
) + αI
i
(a
J
k
0
,E
) ≤ (1 +
α)I
i
(V), and for high-value user i we use the bound
E
β
I
i
(a
J
k
,E
) + αI
i
(a
J
k
0
,E
)
(a)
= (1 + α)
1
2
E
β
−i
I
i
(a
J
1
,E
)
+
1
2
E
β
−i
I
i
(a
J
2
,E
)
(b)
≥
1 + α
2
E
β
−i
h
I
i
(V
(l)
∩ J
1
)
i
+ E
β
−i
h
I
i
(V
(l)
∩ J
2
)
i
=
1 + α
2
E
β
−i
h
I
i
(V
(l)
∩ J
1
) + I
i
V
(l)
\
V
(l)
∩ J
1
i
(c)
≥ (1 + α)E
β
−i
1
2
I
i
(V
(l)
)
=
1 + α
2
I
i
(V
(l)
).
where (a) follows from the fact that we have uniform mixed joining strategy, (b) follows from the
fact that on each platform all low-value users share their information, and (c) follows from the fact
that leaked information is submodular.
Existence of Mixed Strategy Equilibria when Platforms Compete over Data Prices
Our main existence result in the case of competition over data prices is:
Theorem B-2. There exists a mixed strategy equilibrium strategy.
This theorem follows because for any price vector p
1
and p
2
, the second-stage game is a finite
game and therefore has a mixed strategy equilibrium. If there are multiple equilibria, we select
the one with the highest sum of platform’s utilities. We next establish the existence of the mixed
strategy equilibirium in the first-stage game by using Dasgupta-Maskin theorem stated below.
Theorem B-3 (Dasgupta and Maskin [1986]). Consider a game with n players where the action space of
user i is denoted by a bounded set S
i
and her payoff is denoted by u
i
. If
B-6
1. for any i, u
i
is continuous except on a subset of S
∗
(i), where S
∗
(i) = {s ∈ S : ∃j 6= i such that s
j
=
f
d
ij
(s
i
)}, for bijective and continuous functions f
d
ij
: S
i
→ S
j
for d = 1, . . . , D(i).
2.
P
N
i=1
u
i
(s) is upper semicontinuous, i.e., for any sequence s
k
→ s, we have
P
N
i=1
u
i
(s) ≥ lim sup
k→∞
P
N
i=1
u
i
(s
k
).
3. for any i, u
i
(s
i
, s
−i
) is weakly lower semicontinuous, i.e., there exists λ ∈ [0, 1] such that λ lim inf
s
0
i
↑s
i
u
i
(s
0
i
, s
−i
)+
(1 − λ) lim inf
s
0
i
↓s
i
u
i
(s
0
i
, s
−i
) ≥ u
i
(s
i
, s
−i
).
Then a mixed strategy equilibrium exists.
We next show that the conditions of this theorem are satisfied, establishing a mixed strategy
equilibrium exists. First, note that the price each platform offers to any user cannot exceed the
highest overall leaked information, i.e.,
P
i∈V
I
i
(V). Therefore, without loss of generality, we as-
sume the action space of both platforms is [0,
P
i∈V
I
i
(V)]
n
.
For two vector of prices p
1
and p
2
and user i ∈ V we define functions f
12
: p
1
→ p
2
such that
[f
12
(p
1
)]
i
= p
1
i
− v
i
I
i
(S
1
) + c
i
(J
1
) + v
i
I
i
(S
2
) − c
i
(J
2
), ∀S
1
, S
2
, J
1
, J
2
⊆ V.
Note that there are finitely many such functions and in particular at most n
2
n
×2
n
×2
n
of them (this
is because there are n components and for each of them J
1
has 2
n
possibilities, J
2
= V\J
1
, and each
of S
1
and S
2
have 2
n
possibilities). Also, note that the functions f
12
are all linear and hence bijective
and continuous. By changing the prices p
1
and p
2
, as long as user equilibria of the second-stage
game are the same, the payoff functions remain continuous. It becomes discontinuous when a
user i ∈ V who is sharing on platform 1 changes her decision and starts sharing on platform 2.
For this to happen we must have p
1
i
− v
i
I
i
(S
1
) + c
i
(J
1
) = p
2
i
− v
i
I
i
(S
2
) + c
i
(J
2
), where S
1
is the set
of users who are sharing on platform 1, S
2
is the set of users who are sharing on platform 2, and
J
1
and J
2
are the sets of users who are joining platforms 1 and 2, respectively. Therefore, for any
discontinuity point of U
1
(p
1
, p
2
), there exists f
12
such that p
2
= f
12
(p
1
). This establishes that the
first condition of Theorem B-3 holds.
The second condition of Theorem B-3 holds because as long as user equilibria of the second-
stage game remains the same, payoff functions are continuous in the first stage prices. When user
equilibria changes, we select the one with the highest sum of the platforms’ utilities. This implies
that the sum of platforms’ utilities is an upper semicontinuous function in prices.
The third condition of Theorem B-3 holds because by changing p
1
, as long as the equilibrium
of the second-stage game has not changed, the payoff of platform 1 is continuous. At the point
that the equilibrium changes, we have multiplicity of equilibria and we have chosen the one that
gives maximum payoff of platforms. Therefore, we have lim inf
p
01
↓p
1
U
1
(p
01
, p
2
) = U
1
(p
1
, p
2
),
which by definition is weakly lower semicontinuous with the choice of λ = 0.
Proof of Theorem 8
Part 1: In this case, there is no externality among users, and both the first best and the equilibrium
involve all users joining platform 1 (or platform 2) and all low-value users sharing their data.
B-7

In particular, we show that the following prices with a user equilibrium in which all users join
platform 1 and all low-value users share on platform 1 is an equilibrium. For all i ∈ V
(l)
we let
p
1,E
i
=
v
i
I
i
({i}), c
i
(V) − c
i
({i}) ≥ (1 − v
i
)I
i
({i}),
I
i
({i}) − (c
i
(V) − c
i
({i})) , c
i
(V) − c
i
({i}) < (1 − v
i
)I
i
({i}),
and
p
2,E
i
=
v
i
I
i
({i}), c
i
(V) − c
i
({i}) ≥ (1 − v
i
)I
i
({i}),
I
i
({i}), c
i
(V) − c
i
({i}) < (1 − v
i
)I
i
({i}).
This is a user equilibrium because the payoff of a user on platform 1 is c
i
(V) that is larger than
her payoff on platform 2 which is c
i
({i}). We next show that platform 1 does not have a profitable
deviation. For any user i for which c
i
(V) − c
i
({i}) ≥ (1 − v
i
)I
i
({i}) platform 1 cannot increase
its payoff by reducing its price offer because the user would then stop sharing her data. For any
user with c
i
(V) − c
i
({i}) < (1 − v
i
)I
i
({i}), a lower price would make the user join platform 2. This
establishes that the first platform does not have a profitable deviation. We next show that platform
2 does not have a profitable deviation. The maximum price that platform 2 can offer to user i
without making negative profits is I
i
({i}) (this is because there exists no externality). Such a price
offer is not sufficient to attract users from platform 1. In particular, if c
i
(V)−c
i
({i}) < (1−v
i
)I
i
({i})
then the price I
i
({i}) offered to user i by the second platform would make her indifferent between
the two platforms and if c
i
(V) − c
i
({i}) ≥ (1 − v
i
)I
i
({i}) then the price I
i
({i}) offered to user i by
the second platform would give her a lower payoff. Therefore, the second platform does not have
a profitable deviation. This completes the proof of the first part.
Part 2: Note that the first best is to have all users join the same platform and low-value users share
on it, which we assume is platform 1. Since there is no externality from high-value users, without
loss of generality, we show the proof when they are removed from the market as they will join
(and not share) the platform that has a higher joining value for them.
Part 2-1: We show that if δ ≥ δ
for
δ = max
i∈V
X
j∈V
I
j
(V)
+ v
i
(I
i
(V \ {i}) − I
i
({i})), (B-5)
the first best is an equilibrium, supported by the following prices:
p
1,E
i
= v
i
(I
i
(V) − I
i
(V \ {i})), i ∈ V (B-6)
p
2,E
i
= c
i
(V) − c
i
({i}) − v
i
I
i
(V \ {i}) + v
i
I
i
({i}), i ∈ V.
Note that all (low-value) users joining and sharing on platform 1 is a user equilibrium. This is
because the payoff of each user i is she deviates and shares on the other platform is equal to her
current payoff. Platform 1 does not have a profitable deviation. This is because, using Theorem 2,
B-8

platform 1 is paying the minimum prices to get the data of all users. We next show that platform 2
does not have a profitable deviation, establishing the prices specified above and all users sharing
on platform 1 is an equilibrium. The highest price that platform 2 can offer to get one of users, e.g.,
user i, share on it is bounded by the total information leakage
P
j∈V
I
j
(V). We show that given
the condition on δ all users joining and sharing on platform 1 is always a user equilibrium which
gives the second platform zero payoff. Consider user i ∈ V, given all other users are sharing on
platform 1 it is best response for this user to share on platform 1 because
p
1,E
i
− v
i
I
i
(V) + c
i
(V)
(a)
= −v
i
I
i
(V \ {i}) + c
i
(V)
(b)
≥ −v
i
I
i
(V \ {i}) + δ + c
i
({i})
(c)
≥
X
j∈V
I
j
(V) − v
i
I
i
({i}) + c
i
({i}) ≥ ˜p
2
i
− v
i
I
i
({i}) + c
i
({i}).
where (a) follows from plugging in the prices given in (B-6), (b) follows from the definition of δ,
and (c) follows from (B-5).
Part 2-2: We show that given ∆ ≤
¯
∆ and v
i
≤ ¯v, where
¯
∆ = max
max
i,S: i6∈S
(1 − v
i
)I
i
(V) + v
i
(2I
i
({i}) − I
i
(S
c
)), (B-7)
max
S⊆V
1
2|S|
X
i∈S
I
i
(V) − (1 − v
i
)I
i
(S) − v
i
I
i
(S
c
∪ {i})
. (B-8)
and
¯v = min
1
2
, min
i,S: i∈S,I
i
(V)−I
i
(S)6=0
I
i
(V) − I
i
(S)
I
i
(V) − I
i
(S) + I
i
(S
c
∪ {i}) − I
i
({i})
. (B-9)
the first best is an equilibrium.
Before we proceed with the proof of this case, note that both
¯
∆ and ¯v are non-zero. The latter is
by hypothesis. Consider the former, (B-7). The first term on the right-hand side of this expression
is non-zero if v
i
≤
1
2
. The second term on the right-hand side of this expression is non-zero,
because v
i
≤ 1 and leaked information is monotonically increasing in the set of users who share.
If I
i
(V) = I
i
(S) for some S, then user i is uncorrelated with users and the complement of S, S
c
.
If I
i
(V) = I
i
(S
c
) for some S, then user i is uncorrelated with users in S. Therefore, for the right-
hand side of the above expression to be zero all users must be uncorrelated with all other users.
But this contradicts the assumption that at least the data of two low-value users are correlated.
We next show that the following prices form an equilibrium:
p
1,E
i
= I
i
(V) − (c
i
(V) − c
i
({i})), i ∈ V, (B-10)
p
2,E
i
= (1 − v
i
)I
i
(V) + I
i
({i}), i ∈ V. (B-11)
Note that with these prices all users sharing on platform 1 is a user equilibrium. This is because if a
user deviates and shares on the second platform, she receives the same payoff. We next show that
B-9
the second platform does not have a profitable deviation. Suppose the second platform deviates to
get users in a set S share on it by offering prices ˜p
2
i
. We show that the payoff of platform 2 becomes
strictly negative. Consider one of the user equilibria after this deviation and suppose that the set
J
1
⊆ S
c
of users join platform 1 and a subset of J
1
, S
1
, shares on platform 1. Users in S must prefer
to share on platform 2, which leads to ˜p
2
i
− v
i
I
i
(S) + c
i
(S) ≥ p
i
1
− v
i
I
i
(S
1
∪ {i}) + c
i
(J
1
∪ {i}) ≥
I
i
(V) − (c
i
(V) − c
i
({i})) − v
i
I
i
(S
c
∪ {i}) + c
i
({i}). Hence
˜p
2
i
≥ v
i
I
i
(S) − c
i
(S) + I
i
(V) − (c
i
(V) − c
i
({i})) − v
i
I
i
(S
c
∪ {i}) + c
i
({i})
(a)
≥ −2∆ + I
i
(V) + v
i
I
i
(S) − v
i
I
i
(S
c
∪ {i}). (B-12)
Therefore, the payoff of platform 2 becomes
X
i∈S
I
i
(S) − ˜p
2
i
(a)
≤
X
i∈S
I
i
(S) + 2∆ − I
i
(V) − v
i
I
i
(S) + v
i
I
i
(S
c
∪ {i})
= 2∆|S| +
X
i∈S
(1 − v
i
)I
i
(S) + v
i
I
i
(S
c
∪ {i}) − I
i
(V)
(b)
< 0,
where (a) follows by using (B-12) and (b) follows from the choice of
¯
∆ given in (B-7).
We next show that platform 1 does not have a profitable deviation. Suppose that platform
1 deviates to get users in the set S to share on it with prices ˜p
1
i
. We first claim that if ∆ ≤
¯
∆
(where
¯
∆ is given in (B-7)), in one of the user equilibria all users prefer to share on platform 2. In
particular, for a user i ∈ S
c
, her payoff if she shares on platform 2 is higher than her payoff if she
joins platform 2 and does not share because
p
2
i
− v
i
I
i
(S
c
) + c
i
(S
c
)
(a)
= (1 − v
i
)I
i
(V) + v
i
I
i
({i}) − v
i
I
i
(S
c
) + c
i
(S
c
)
(b)
≥ −v
i
I
i
(S
c
\ {i}) + c
i
(S
c
),
where (a) follows by using the prices given in (B-10) and (b) follows the submodularity of leaked
information and in particular v
i
I
i
({i}) ≥ v
i
(I
i
(S
c
) − I
i
(S
c
\ {i})). Also, for a user i ∈ S
c
, her
payoff if she shares on platform 2 is higher than her payoff if she joins platform 1 because (she
does not share on platform 1 as the price offered to her is 0)
p
2
i
− v
i
I
i
(S
c
) + c
i
(S
c
)
(a)
= (1 − v
i
)I
i
(V) + v
i
I
i
({i}) − v
i
I
i
(S
c
) + c
i
(S
c
)
(b)
≥ (1 − v
i
)I
i
(V) + v
i
I
i
({i}) − v
i
I
i
(S
c
) + c
i
(S ∪ {i}) − ∆
(c)
≥ −v
i
I
i
({i}) + c
i
(S ∪ {i}) ≥ −v
i
I
i
(S ∪ {i}) + c
i
(S ∪ {i})
where (a) follows by using the prices given in (B-10), (b) follows from the definition of ∆, (c)
follows from the choice of
¯
∆ given in (B-7). To have users in the set S share on platform 1 the new
B-10

prices must satisfy
˜p
1
i
− v
i
I
i
(S) + c
i
(S) ≥ p
2
i
− v
i
I
i
(S
c
∪ {i}) + c
i
(S
c
∪ {i})
(a)
= (1 − v
i
)I
i
(V) + v
i
I
i
({i}) − v
i
I
i
(S
c
∪ {i}) + c
i
(S
c
∪ {i}),
where (a) follows from substituting for prices from (B-10). Therefore,
˜p
1
i
≥ (1 − v
i
)I
i
(V) + v
i
I
i
({i}) − v
i
I
i
(S
c
∪ {i}) + v
i
I
i
(S) + c
i
(S
c
∪ {i}) − c
i
(S)
≥ (1 − v
i
)I
i
(V) + v
i
I
i
({i}) − v
i
I
i
(S
c
∪ {i}) + v
i
I
i
(S) − ∆. (B-13)
We next show that this user equilibrium generates no higher payoff for platform 1 (compared to
its equilibrium payoff of ∆|V|). In particular, the payoff of platform 1 can be written as
X
i∈S
I
i
(S) − ˜p
1
i
(a)
≤
X
i∈S
(1 − v
i
)I
i
(S) − (1 − v
i
)I
i
(V) + v
i
I
i
(S
c
∪ {i}) − v
i
I
i
({i}) + ∆
(b)
≤ ∆|S| ≤ ∆|V|
where in (a) we used the inequality (B-13), and (b) follows from the choice of ¯v given in (B-9). In
particular, using v
i
≤ ¯v, for any i and S such that I
i
(V) − I
i
(S) 6= 0, we have (1 − v
i
)I
i
(S) − (1 −
v
i
)I
i
(V) + v
i
I
i
(S
c
∪ {i}) − v
i
I
i
({i}) ≤ 0. For any S and i ∈ S for which I
i
(V) − I
i
(S) = 0, user
i’s data must be independent of the data of users in S
c
. Therefore, we have I
i
(S
c
∪ {i}) = I
i
({i}).
This leads to
(1 − v
i
)I
i
(S) − (1 − v
i
)I
i
(V) + v
i
I
i
(S
c
∪ {i}) − v
i
I
i
({i}) = 0.
This completes the proof of this case.
Part 2-3: We show that if ∆ ≤
˜
∆ where
˜
∆ = min
min
i∈V
1
2
(1 − v
i
)I
i
({i}), max
i∈V
P
i6=j
I
i
({i, j}) − I
i
({i})
2(3|V| − 2)
, (B-14)
then there exist
˜
v such that for v
(l)
≥
˜
v the equilibrium is inefficient.
Before, we proceed with the proof, note that the second argument of maximum is non-zero
since there exits at least two low-value users whose data are correlated.
We show that there exists no prices for both platforms to sustain all (low-value) users share
on platform 1 as an equilibrium. We suppose the contrary and then reach a contradiction. In
particular, we let x
1
, . . . , x
n
and y
1
, . . . , y
n
be the equilibrium prices offered by platform 1 and 2.
Since all users sharing on platform 1 is a user equilibrium we must have x
i
− v
i
I
i
(V) + c
i
(V) ≥
y
i
− v
i
I
i
({i}) + c
i
({i}). Also, note that we must have x
i
− v
i
I
i
(V) ≤ c
i
(V) − c
i
({i}) + y
i
− v
i
I
i
({i}).
This is because, otherwise platform 1 can deviate by decreasing its prices and increase its payoff.
Therefore, we have
x
i
− v
i
I
i
(V) ∈ [−(c
i
(V) − c
i
({i})) + y
i
− I
i
({i}), (c
i
(V) − c
i
({i})) + y
i
− I
i
({i})] , i ∈ V. (B-15)
B-11

Moreover, we also have
x
i
− v
i
I
i
(V) + c
i
(V) ≥ (1 − v
i
)I
i
({i}) + c
i
({i}), i ∈ V. (B-16)
This is because if this inequality does not hold for some i ∈ V, i.e., = ((1 − v
i
)I
i
({i}) + c
i
({i})) −
(x
i
−v
i
I
i
(V)+c
i
(V)) > 0, then platform 2 will have a profitable deviation by letting y
0
i
= I
i
({i})−
2
for all i ∈ V. This is because in any user equilibria after this deviation at least one user shares on
this platform, guaranteeing a positive profit.
We now consider the deviation of platform 1. For any j ∈ V, the following prices guarantee
that the only user equilibria is to have all users i in V \ {j} to share on platform 1 and user j share
on platform 2:
x
0
i
= c
i
(V) − c
i
({i}) + y
i
− v
i
I
i
({i, j}) + v
i
I
i
(V \ {j}) + ∆, i ∈ V \ {j},
This is a user equilibrium because for any user i ∈ V \ {j} the price offered to her with the
maximum leaked information on platform 1 and minimum joining value is larger than her payoff
with the price offered on platform 2 with minimum leaked information and maximum joining
value, i.e., we have
x
0
i
− v
i
I
i
(V \ {j}) + c
i
({i}) > y
i
− v
i
I
i
({i, j}) + c
i
(V).
Also, user j shares on platform 2 because we have
y
j
− v
j
I
j
({j}) + c
j
({j})
(a)
≥ x
j
− v
j
I
j
(V) − c
j
(V) + c
j
({j}) + c
j
({j})
(b)
≥ (1 − v
j
)I
j
({j}) + 2(c
j
({j}) − c
j
(V)) + c
j
({j})
(c)
≥ (1 − v
j
)I
j
({j}) − 2∆ + c
j
({j})
(d)
≥ c
j
({j})
where (a) follows from (B-15), (b) follows from (B-16), (c) follows from the definition of ∆, and (d)
follows from condition (B-14).
This should not be a profitable deviation for platform 1, which leads to
X
i6=j
I
i
(V \ {j}) − x
0
i
=
X
i6=j
I
i
(V \ {j}) − c
i
(V) + c
i
({i}) − y
i
+ v
i
I
i
({i, j}) − v
i
I
i
(V \ {j})
(a)
=
X
i6=j
I
i
(V \ {j}) − 2c
i
(V) + 2c
i
({i}) − x
i
− ∆ + v
i
(I
i
(V) − I
i
({i}) + I
i
({i, j}) − I
i
(V \ {j}))
(b)
≤
X
i∈V
I
i
(V) − x
i
,
where in (a) we used (B-15), and in (b) we used the fact that in the only user equilibrium after this
deviation the payoff of platform 1 cannot increase. Rearranging the previous inequality and using
B-12

the definition of ∆, for any j ∈ V we obtain
x
j
≤ I
j
(V) +
X
i6=j
(1 − v
i
) (I
i
(V) − I
i
(V \ {j})) + v
i
(I
i
({i}) − I
i
({i, j})) + 3∆, j ∈ V. (B-17)
We now consider the deviation of platform 2. In particular, we show that for any j ∈ V, with
price y
0
j
= x
j
− v
j
I
j
(V) + c
j
(V) + v
j
I
j
({j}) − c
j
({j}) + ∆ and zero for all other users the only user
equilibrium is to have user j share on platform 2 and all other users share on platform 1. First note
that all other users will still share on platform 1 as their information leakage has weakly decreased
(since j is not sharing on platform 1) and they receive the same payment. now consider user j.
She shares her data on platform 2, because with the choice of the price y
0
j
we have y
0
j
− v
j
I
j
({j}) +
c
j
({j}) > x
j
− v
j
I
j
(V) + c
j
(V). This cannot be a profitable deviation for platform 2 leading to
I
j
({j}) − y
0
j
= I
j
({j}) − x
j
+ v
j
I
j
(V) − v
j
I
i
({j}) ≤ 0. Therefore, we have
x
j
≥ (1 − v
j
)I
j
({j}) + v
j
I
j
(V) − ∆. (B-18)
We next show that for sufficiently large v
(l)
given the choice of
˜
∆, the inequalities (B-18), and
(B-17) cannot simultaneously hold. In particular, consider j ∈ V who is with at least one other
low-value user. For boundary low-values, i.e., v
i
= 1, we must have ∆(3|V| − 2) + I
j
(V) +
P
i6=j
(I
i
({i}) − I
i
({i, j})) ≥ I
j
(V), which does not hold provided that ∆ <
1
3|V|−2
P
i6=j
I
i
({i, j})−
I
i
({i}). Since ∆ ≤
˜
∆ for sufficiently large values v
(l)
, there exists no prices for which the first best
can be sustained as an equilibrium, establishing inefficiency in this case.
Part 3-1: We first show that there exists
¯
v and v such that if v
(h)
≥
¯
v, v
(l)
≥ v, and
δ >
1
|V|
X
i∈V
(l)
(1 − v
i
)(I
i
(V
(l)
) − I
i
(V
(l)
1
)), (B-19)
the first best is to have all users joining the same platform, say platform 1, and only low-value
users who are not correlated with high-value users share their data. Let V
(l)
1
= {i ∈ V
(l)
: ∀j ∈
V
(h)
, Σ
ij
= 0}, be those low-value users uncorrelated with all high-value users and V
(l)
2
= V \ V
(l)
2
to denote the rest of the low-value users (i.e., low-value users correlated with at least one high-
value user). The first best is to have all users join one of the platforms, say platform 1, because we
can upper bound the social surplus when set J
k
(6= ∅ and 6= V) joins platform k ∈ {1, 2} and set S
k
share on it as
X
i∈J
1
(1 − v
i
)I
i
(S
1
) + c
i
(J
1
) +
X
i∈J
2
(1 − v
i
)I
i
(S
2
) + c
i
(J
2
)
(a)
≤ −|V|δ +
X
i∈V
c
i
(V) +
X
i∈J
1
(1 − v
i
)I
i
(S
1
) +
X
i∈J
2
(1 − v
i
)I
i
(S
2
)
(b)
≤ −|V|δ +
X
i∈V
c
i
(V) +
X
i∈J
1
∩V
(l)
(1 − v
i
)I
i
(S
1
∩ V
(l)
) +
X
i∈J
2
∩V
(l)
(1 − v
i
)I
i
(S
2
∩ V
(l)
)
B-13

≤ −|V|δ +
X
i∈V
c
i
(V) +
X
i∈V
(l)
(1 − v
i
)I
i
(V
(l)
)
(c)
≤
X
i∈V
c
i
(V) +
X
i∈V
(l)
1
(1 − v
i
)I
i
(V
(l)
1
),
where (a) follows from the definition of δ, (b) follows from the fact that for sufficiently large ¯v only
low-value users share and the information leakage of high-value users is zero, and (c) follows from
condition (B-19). We next consider two possible cases and show that in both of them platform 2
has a profitable deviation.
Case 1: There exists no non-zero correlation between users in V
(l)
1
and users in V
(l)
2
. We show that
in this case platform 2 can induce all users in V
(l)
2
to join and share their data. In particular, the
following prices form a profitable deviation for platform 2:
˜p
2
i
= ∆ + v
i
I
i
(V
(l)
2
), i ∈ V
(l)
2
,
and zero price to all other users. We first show that with these prices in any user equilibrium all
users in V
(l)
2
will join and share on platform 2. This is because the payoff of a user i ∈ V
(l)
2
after
deviating to share on platform 2 is
˜p
2
i
− v
i
I
i
(S
2
∪ {i}) + c
i
(J
2
∪ {i})
(a)
≥ ˜p
2
i
− v
i
I
i
(V
(l)
2
) + c
i
(J
2
∪ {i})
(b)
= ∆ + c
i
(J
2
∪ {i})
(c)
≥ c
i
(J
1
∪ {i})
where (a) follows from the fact that the price offered by platform 2 to users outside of V
(l)
2
is zero
and hence they never share on platform 2, (b) follows from the choice of price offered by platform
2, and (c) follows from the definition of ∆. We next show that if
X
i∈V
(l)
2
(1 − v
i
)I
i
(V
(l)
2
) > ∆|V
(l)
2
|, (B-20)
then the payoff of platform 2 after this deviation becomes strictly positive. Note that we can lower
bound the payoff of platform 2 by
X
i∈V
(l)
2
I
i
(V
(l)
2
) − ˜p
2
i
=
X
i∈V
(l)
2
I
i
(V
(l)
2
) − ∆ − v
i
I
i
(V
(l)
2
) =
X
i∈V
(l)
2
(1 − v
i
)I
i
(V
(l)
2
) − ∆|V
(l)
2
| > 0.
Finally, we show that there exist
¯
δ and
¯
∆ such that for δ ≥
¯
δ and ∆ ≤
¯
∆ both (B-19) and (B-20)
hold. First note that since in this case users in V
(l)
1
and those in V
(l)
2
are uncorrelated, condition (B-
19) becomes δ >
1
|V|
P
i∈V
(l)
2
(1−v
i
)I
i
(V
(l)
2
). Therefore, letting ∆ <
¯
∆ =
1
|V
(l)
2
|
P
i∈V
(l)
2
(1−v
i
)I
i
(V
(l)
2
),
and δ >
¯
δ =
1
|V
(l)
|
P
i∈V
(l)
2
(1 − v
i
)I
i
(V
(l)
2
), completes the proof in this case.
Case 2: There exists j ∈ V
(l)
2
who is correlated with at least one other user in V
(l)
1
. We show that
platform 2 has a profitable deviation to take user j join and share on it. In particular, the following
prices constitute a profitable deviation for platform 2:
˜p
2
j
= c
j
(V) − c
j
({j}) + v
j
I
j
({j}) − v
j
I
j
(V
(l)
1
),
B-14

and zero price to all other user. First note that in any user equilibrium user j shares on platform
2. This is because ˜p
2
j
− v
j
I
j
({j}) + c
j
(J
2
∪ {j}) = c
j
(V) − c
j
({j}) − v
j
I
j
(V
(l)
1
) + + c
j
(J
2
∪ {j}) ≥
c
j
(V) − v
j
I
j
(V
(l)
1
). This deviation is profitable for platform 2 provided that
(1 − v
j
)I
j
({j}) + v
j
I
j
(V
(l)
1
) > ∆. (B-21)
Note that in this case I
j
(V
(l)
1
) > 0. Letting
¯
∆ = I
j
(V
(l)
1
) ≥ ∆ and
¯
δ =
1
|V
(l)
|
P
i∈V
(l)
2
(1 − v
i
)I
i
(V
(l)
2
) <
δ, guarantees that the first best is not an equilibrium. The proof is completed by observing that for
v
(l)
sufficiently close to 1, we have
¯
∆ >
¯
δ.
Part 3-2: We prove that for
δ >
˜
δ = max
i∈V
v
i
I
i
(V) +
X
j∈V
I
j
(V), (B-22)
the first best is an equilibrium.
We first show that when δ is large, the first best involves all users joining the same platform,
say platform 1. This is proved by showing that if users split and join different platforms social
surplus decreases. Let J
1
6= ∅, V be the set of users who join platform 1 and J
2
be the set of users
who join platform 2. Also, let S
1
and S
2
be the sets of users who share on platforms 1 and 2,
respectively. We can upper bound the surplus as
X
i∈J
1
c
i
(J
1
) + (1 − v
i
)I
i
(S
1
)
+
X
i∈J
2
c
i
(J
2
) + (1 − v
i
)I
i
(S
2
)
(a)
≤
X
i∈V
c
i
(V) − δ
!
+
X
i∈J
1
(1 − v
i
)I
i
(S
1
) +
X
i∈J
2
(1 − v
i
)I
i
(S
2
)
(b)
≤ −δ|V| +
X
i∈V
c
i
(V) + I
i
(V)
(c)
<
X
i∈V
c
i
(V),
where (a) follows from the definition of δ and J
1
, J
2
6= ∅, (b) follows from replacing (1 − v
i
)I
i
(S
k
)
for k = 1, 2 by its upper bound I
i
(V), and (c) follows from the condition given in (B-22). We
next show that the first best, a
W
, can be supported as an equilibrium. In particular, the prices
p
1
i
= v
i
(I
i
(a
W
)−I
i
(a
i
= 0, a
W
−i
)) for all i ∈ V and p
2
i
= 0 for all i ∈ V makes a
W
an equilibrium. We
next verify that at these prices a
W
is indeed a user equilibrium and than that none of the platforms
have a profitable deviation. It is a user equilibrium because the payoff of any user such as user
i on platform 1 is larger than or equal to c
i
(V) − v
i
I
i
(V). If user i deviates and joins platform 2,
then her payoff is smaller than or equal to c
i
({i}) +
P
j∈V
I
j
(V) (because the highest price offered
to users on platform 2 is the total leaked information). User i does not have a profitable deviation
because c
i
(V)−v
i
I
i
(V) > c
i
({i})+δ−v
i
I
i
(V) ≥ c
i
({i})+
P
j∈V
I
j
(V). We next show that platforms
do not have a profitable deviation. Next suppose that platform 1 deviates and offers price vector
˜
p
1
. Since c
i
(V) − v
i
I
i
(V) > c
i
({i}) + δ − v
i
I
i
(V) ≥ c
i
({i}) +
P
j∈V
I
j
(V), all users joining platform
2 is a user equilibrium of the price vectors (
˜
p
1
, p
2
). This user equilibrium gives platform 1 zero
payoff and therefore deviating and offering price vector
˜
p
1
is not profitable for platform 1. The
same argument also establishes that platform 2 does not have a profitable deviation.
B-15
Proof of Proposition 8
We prove that with the price given by p
i
(v) =
I
i
(a(v)) +
P
j6=i
(1 − v
j
)I
j
(a(v))
+ h
i
(v
−i
), for
any function h
i
(·) which depends only on v
−i
where a(v) is defined as
a(v) = argmax
a∈{0,1}
n
X
i∈V
(1 − v
i
)I
i
(a),
the users report their value of privacy truthfully. Consider user i ∈ V and suppose she reports v
0
instead of her true value of privacy v
i
. Her payoff becomes
p
i
(v
0
, v
−i
) − v
i
I
i
(a(v
0
, v
−i
)) =
I
i
(a(v
0
, v
−i
)) +
X
j6=i
(1 − v
j
)I
j
(a(v
0
, v
−i
))
+ h
i
(v
−i
) − v
i
I
i
(a(v
0
, v
−i
))
=
X
j∈V
(1 − v
j
)I
j
(a(v
0
, v
−i
))
+ h
i
(v
−i
)
(a)
≤
X
j∈V
(1 − v
j
)I
j
(a(v
i
, v
−i
))
+ h
i
(v
−i
)
(b)
= p
i
(v) − v
i
I
i
(a(v)),
where inequality (a) follows from the definition of a(v) as the maximizer of the surplus and equal-
ity (b) follows from the definition of a(v) and p(v), and p
i
(v) − v
i
I
i
(a(v)) is equal to the payoff of
user i if she reports truthfully.
Finally, note that with the choice of h
i
(v
−i
) = − min
a∈{0,1}
n
P
j6=i
(1 − v
j
)I
j
(a) + I
i
(a)
the
prices become nonnegative because
p
i
(v) =
I
i
(a(v)) +
X
j6=i
(1 − v
j
)I
j
(a(v))
− min
a∈{0,1}
n
I
i
(a) +
X
j6=i
(1 − v
j
)I
j
(a)
≥ 0.
Proof of Theorem 9
Using the revelation principle, we can focus on direct mechanisms and then find the optimal
direct incentive compatible mechanism. For the given prices, users in the set a(v) share their data.
Letting A
i
(v, v
−i
) = I
i
(a(v, v
−i
)) − I
i
(a
i
= 0, a
−i
(v, v
−i
)), the incentive compatibility constraint
can be written as
p
i
(v, v
−i
) − vA
i
(v, v
−i
) ≥ p
i
(v
0
, v
−i
) − vA
i
(v
0
, v
−i
). (B-23)
Writing the first order condition for inequality (B-23) yields p
0
i
(v, v
−i
) = vA
0
i
(v, v
−i
) for all v. Tak-
ing integral of both sides yields
p
i
(v, v
−i
) = −
Z
v
max
v
xA
0
i
(x, v
−i
)dx
(a)
=
Z
v
max
v
A
i
(x, v
−i
)dx + vA
i
(v, v
−i
), (B-24)
where we used integration by part in (a). The expected payment to user i is
E
v∼F
i
[p
i
(v, v
−i
)] =
Z
p
i
(v, v
−i
)f
i
(v)dv
(a)
= −
Z
v
max
0
Z
v
max
v
xA
0
i
(v, v
−i
)dxf
i
(v)dv
B-16

(b)
= −
Z
v
max
0
Z
x
0
xA
0
i
(x, v
−i
)f
i
(v)dvdx = −
Z
v
max
0
F
i
(x)xA
0
i
(x, v
−i
)dx
(c)
=
Z
v
max
0
(f
i
(x)x + F
i
(x))A
i
(x, v
−i
)dx
− F
i
(x)xA
i
(x, v
−i
)|
v
max
0
=
Z
v
max
0
x +
F
i
(x)
f
i
(x)
f
i
(x)A
i
(x, v
−i
)dx.
where (a) follows from equation (B-24), (b) follows from changing the order of integrals, and (c)
follows from integration by part. Therefore, the expected payment to user i becomes E
v
[p
i
(v)] =
E
v
[Φ
i
(v
i
)A
i
(v)]. Therefore, the expected payoff of the platform is
E
v
"
n
X
i=1
I
i
(a(v)) − Φ
i
(v
i
)(I
i
(a(v)) − I
i
(a
i
= 0, a
−i
(v)))
#
.
The equilibrium sharing profile maximizes
n
X
i=1
I
i
(a(v)) − Φ
i
(v
i
) (I
i
(a(v)) − I
i
(a
i
= 0, a
−i
(v)))
=
n
X
i=1
(1 − Φ
i
(v
i
))I
i
(a(v)) + Φ
i
(v
i
)I
i
(a
i
= 0, a
−i
(v)),
for any reported vector v. Finally, note that maximizing this expression yield the following prop-
erty: if a(v, v
−i
) = 1, then for all v
0
≤ v we have a(v
0
, v
−i
) = 1. This follows from the fact that by
Assumption 2 we have Φ
i
(v
0
) ≤ Φ
i
(v) for all v
0
≤ v. Since the leaked information is monotone,
we obtain that A
i
(v, v
i
) is decreasing in v because as we increase v, Φ
i
(v) increases, which means
a
i
(v, v
−i
) decreases, which in turn means that A
i
(v, v
i
) = I
i
(a(v, v
−i
))−I
i
(a
i
= 0, a
−i
(v, v
−i
)) de-
creases. This monotonicity property together with the payment identity (B-24) guarantees that the
incentive compatibility constraint holds as we show next. Using the payment identity (B-24), the
incentive compatibility constraint p
i
(v, v
−i
) − vA
i
(v, v
−i
) ≥ p
i
(v
0
, v
−i
) − vA
i
(v
0
, v
−i
), is equivalent
to
Z
v
max
v
A
i
(x, v
−i
)dx
+vA
i
(v, v
−i
)−vA
i
(v, v
−i
) ≥
Z
v
max
v
0
A
i
(x, v
−i
)dx
+v
0
A
i
(v
0
, v
−i
)−vA
i
(v
0
, v
−i
).
After canceling out the term vA
i
(v, v
−i
) and rearranging the other terms, this inequality becomes
equivalent to
R
v
0
v
A
i
(x, v
−i
)dx ≥ (v
0
− v)A
i
(v
0
, v
−i
). To show this inequality we consider the fol-
lowing two possible cases:
• v
0
≥ v: we have
Z
v
0
v
A
i
(x, v
−i
)dx
(a)
≥
Z
v
0
v
A
i
(v
0
, v
−i
)dx = (v
0
− v)A
i
(v
0
, v
−i
),
where (a) follows from the fact that A
i
(x, v
−i
) is decreasing in x and hence for all x ∈ [v, v
0
]
B-17

we have A
i
(x, v
−i
) ≥ A
i
(v
0
, v
−i
).
• v
0
< v: we have
Z
v
0
v
A
i
(x, v
−i
)dx =
Z
v
v
0
−A
i
(x, v
−i
)dx
(a)
≥
Z
v
v
0
−A
i
(v
0
, v
−i
)dx = (v
0
− v)A
i
(v
0
, v
−i
),
where (a) follows from the fact that A
i
(x, v
−i
) is decreasing in x and hence for all x ∈ [v
0
, v]
we have −A
i
(x, v
−i
) ≥ −A
i
(v
0
, v
−i
).
Proof of Theorem 10
In this proof, we will use the following result, which is similar to Lemma 3 (proof omitted).
Lemma B-1. All users for which we have Φ
i
(v
i
) ≤ 1 share their data in equilibrium.
Part 1: Recall that for any action profile a and set T ⊆ V, a
T
denotes (a
i
: i ∈ T ). Since, high-value
users are uncorrelated with all other users, the first best is to have all low-value users share. This
is because for any sharing profile a ∈ {0, 1}
n
we have
Social surplus(a) =
n
X
i=1
(1 − v
i
)I
i
(a)
(a)
=
X
i∈V
(l)
(1 − v
i
)I
i
(a
V
(l)
) +
X
i∈V
(h)
(1 − v
i
)I
i
(a
{i}
)
(b)
≤
X
i∈V
(l)
(1 − v
i
)I
i
(a
V
(l)
)
(c)
≤
X
i∈V
(l)
(1 − v
i
)I
i
(V
(l)
) = Social surplus(1
V
(l)
),
where (a) holds because high-value users’ data are uncorrelated from all other users, (b) holds
because for high-value users (1 − v
i
)I
i
(a
{i}
) ≤ 0, and (c) holds because the leaked information
is monotone. We next show that in equilibrium only users in V
(l)
Φ
= V
(l)
share their data. Using
Theorem 9, in the equilibrium the platform maximizes
P
n
i=1
(1−Φ
i
(v
i
))I
i
(a)+Φ
i
(v
i
)I
i
(a
−i
, a
i
= 0).
We can write
n
X
i=1
(1 − Φ
i
(v
i
))I
i
(a) + Φ
i
(v
i
)I
i
(a
−i
, a
i
= 0)
(a)
=
X
i∈V
(l)
(1 − Φ
i
(v
i
))I
i
(a
V
(l)
) + Φ
i
(v
i
)I
i
(a
V
(l)
\{i}
)
+
X
i∈V
(h)
(1 − Φ
i
(v
i
))I
i
(a
{i}
)
(b)
≤
X
i∈V
(l)
(1 − Φ
i
(v
i
))I
i
(V
(l)
) + Φ
i
(v
i
)I
i
(V
(l)
\ {i}),
where (a) holds because high-value users’ data are uncorrelated from all other users and (b) holds
because for high-value users (1 − Φ
i
(v
i
))I
i
(a
{i}
) ≤ 0 and for users in V
(l)
Φ
we have replaced their
leaked information by its maximum. This shows that in both equilibrium and first best all users
in V
(l)
= V
(l)
Φ
share their data and no other user shares her data.
Part 2: We let i ∈ V
(l)
Φ
and j ∈ V
(h)
be such that Σ
ij
> 0. Therefore, there exists δ > 0 such that
I
j
(V
(l)
Φ
) = δ > 0. We next show that for v
j
> 1 +
P
i∈V
(l)
σ
2
i
δ
the surplus of the action profile a
E
is
B-18

negative, establishing that it does not coincide with the first best. We have
Social surplus(a
E
) =
X
i∈V
(l)
(1 − v
i
)I
i
(a
E
) +
X
i∈V
(h)
(1 − v
i
)I
i
(a
E
)
(a)
≤
X
i∈V
(l)
(1 − v
i
)σ
2
i
+
X
i∈V
(h)
(1 − v
i
)I
i
(a
E
)
(b)
≤
X
i∈V
(l)
(1 − v
i
)σ
2
i
+ (1 − v
j
)I
j
(V
(l)
Φ
) ≤
X
i∈V
(l)
σ
2
i
+ (1 − v
j
)I
j
(V
(l)
Φ
)
(c)
< 0
where in (a) for users in V
(l)
Φ
we have upper bounded the leaked information with its maximum,
in (b) we have removed all the negative terms in the second summation except for the one corre-
sponding to j for which we have replaced leaked information (of equilibrium action profile) by its
minimum (using Lemma B-1), and in (c) we have used v
j
> 1 +
P
i∈V
(l)
σ
2
i
δ
.
Part 3: First note that for sufficiently large
¯
v, all users who are correlated with at least one of the
high-value users do not share in the first best, and let this first best profile denoted by a. Since
user i is correlated with some of the high-value users, in the first best user i ∈ V
(l)
\ V
(l)
Φ
does not
share and we also have
X
j∈V
(h)
I
j
(a) = 0. (B-25)
We next show that for sufficiently small ¯v
i
the action profile a cannot be equilibrium. Using The-
orem 9, in the equilibrium the platform maximizes
P
n
i=1
(1 − Φ
i
(v
i
))I
i
(a) + Φ
i
(v
i
)I
i
(a
−i
, a
i
= 0).
We show that the action profile a
0
= (a
−i
, a
i
= 1) leads to a higher
P
n
i=1
(1 − Φ
i
(v
i
))I
i
(a) +
Φ
i
(v
i
)I
i
(a
−i
, a
i
= 0). We can write
n
X
j=1
(1 − Φ
j
(v
j
))I
j
(a
0
) + Φ
j
(v
j
)I
j
(a
0
−j
, a
j
= 0)
−
n
X
j=1
(1 − Φ
j
(v
j
))I
j
(a) + Φ
j
(v
j
)I
j
(a
−j
, a
j
= 0)
=
X
j∈V\{i}
I
j
(a
i
= 1, a
−i
) − I
j
(a
i
= 0, a
−i
)
+ ((1 − Φ
i
(v
i
))I
i
(a
i
= 1, a
−i
) − (1 − Φ
i
(v
i
))I
i
(a
i
= 0, a
−i
))
−
X
j∈V\{i}
Φ
j
(v
j
)
I
j
(a
0
) − I
j
(a
0
−j
, a
j
= 0)) − I
j
(a) + I
j
(a
−j
, a
j
= 0)
(a)
≥
X
j∈V\{i}
I
j
(a
i
= 1, a
−i
) − I
j
(a
i
= 0, a
−i
)
+ ((1 − Φ
i
(v
i
))I
i
(a
i
= 1, a
−i
) − (1 − Φ
i
(v
i
))I
i
(a
i
= 0, a
−i
))
(b)
≥
X
j∈V
(h)
I
j
({i})
+ (1 − Φ
i
(v
i
))I
i
({i})
(c)
> 0,
where (a) follows from submodularity of leaked information, (b) follows from equation B-25 to-
gether with submodularity of leaked information and the fact that 1 − Φ
i
(v
i
) < 0, and (c) follows
by letting Φ
i
(v
i
) ≤ 1 +
P
j∈V
(h)
I
j
({i})
I
i
({i})
. Letting ˜v be the minimum of Φ
−1
i
1 +
P
j∈V
(h)
I
j
({i})
I
i
({i})
over
all i ∈
ˆ
V
(l)
, completes the proof of this part.
B-19

Part 4: Let i, k ∈ V
(h)
be such that Σ
ik
> 0. First, note that in the first-best solution none of the high-
value users share. We next show that if the value of privacy for high-value user i is small enough,
then at least one high-value user shares in equilibrium. This establishes that any equilibrium is not
efficient. We show this by assuming the contrary and then reaching a contradiction. Suppose that
none of high-value users share. We show that if user i shares, the objective
P
n
i=1
(1−Φ
i
(v
i
))I
i
(a)+
Φ
i
(v
i
)I
i
(a
−i
, a
i
= 0) increases. We let a ∈ {0, 1}
n
denote the equilibrium sharing profile and a
0n
be the same actions profile except that user i is also sharing in a
0
. Using this notation, let us write
n
X
i=1
(1 − Φ
i
(v
i
))I
i
(a
0
) + Φ
i
(v
i
)I
i
(a
0
−i
, a
i
= 0) −
n
X
i=1
(1 − Φ
i
(v
i
))I
i
(a) + Φ
i
(v
i
)I
i
(a
−i
, a
i
= 0)
!
=
X
j∈V\{i}
I
j
(a
i
= 1, a
−i
) − I
j
(a
i
= 0, a
−i
)
+ ((1 − Φ
i
(v
i
))I
i
(a
i
= 1, a
−i
) − (1 − Φ
i
(v
i
))I
i
(a
i
= 0, a
−i
))
−
X
j∈V\{i}
Φ
j
(v
j
)(I
j
(a
0
) − I
j
(a
0
−j
, a
j
= 0)) − Φ
j
(v
j
)(I
j
(a) − I
j
(a
−j
, a
j
= 0))
(a)
≥
X
j∈V\{i}
I
j
(a
i
= 1, a
−i
) − I
j
(a
i
= 0, a
−i
)
+ (1 − Φ
i
(v
i
)) (I
i
(a
i
= 1, a
−i
) − I
i
(a
i
= 0, a
−i
))
(b)
≥
X
j∈V
(h)
I
j
({i})
+ (1 − Φ
i
(v
i
)) (I
i
(a
i
= 1, a
−i
) − I
i
(a
i
= 0, a
−i
))
(c)
≥
X
j∈V
(h)
I
j
({i})
+ (1 − Φ
i
(v
i
))I
i
({i})
(d)
> 0,
where (a) follows from the submodularity of leaked information, (b) follows from the fact that in
the first best action profile a the leaked information of high-value users are zero, (c) follows from
submodularity of leaked information and the fact that 1 − Φ
i
(v
i
) < 0, and (d) follows by letting
Φ
i
(v
i
) < 1 +
P
j∈V
(h)
I
j
({i})
I
i
({i})
. The proof is completed by letting ¯v
i
= Φ
−1
1 +
P
j∈V
(h)
I
j
({i})
I
i
({i})
.
Proof of Proposition 10
We first show that for any user i ∈ V for which a
W
i
= 0, we have a
E
i
= 0. Suppose the contrary, i.e.,
a
W
i
= 0 and a
E
i
= 1. From the choice of taxation policy, since a
W
i
= 0, we have a non-zero tax on
user i’s data. We next compare the platform’s payoff with and without user i’s data and show that
the sharing profile a
E
in which a
E
i
= 1 cannot be equilibrium. Using the price characterization of
Theorem 2,
U(a
E
−i
, a
E
i
= 1, p
a
E
) − U(a
E
−i
, a
E
i
= 0, p
a
i
=0,a
E
−i
)
B-20
=
n
X
j=1
(1 − v
j
)I
j
(a
E
−i
, a
i
= 1) + v
j
I
j
(a
E
−{i,j}
, a
j
= 0, a
i
= 1)
− t
i
−
n
X
j=1
(1 − v
j
)I
j
(a
E
−i
, a
i
= 0) + v
j
I
j
(a
E
−{i,j}
, a
j
= 0, a
i
= 0)
(a)
≤ −t
i
+
X
i :v
j
≤1
σ
2
j
+
X
j :v
j
>1
v
j
σ
2
j
(b)
< 0,
where (a) follows from the fact that for v
j
≤ 1, we have (1 − v
j
)I
j
(a
E
−i
, a
i
= 1) + v
j
I
j
(a
E
−{i,j}
, a
j
=
0, a
i
= 1) ≤ I
j
(a
E
−i
, a
i
= 1) ≤ σ
2
j
and (1 − v
j
)I
j
(a
E
−i
, a
i
= 0) + v
j
I
j
(a
E
−{i,j}
, a
j
= 0, a
i
= 0) ≥ 0.
Also, for v
j
≥ 1 we have (1 − v
j
)I
j
(a
E
−i
, a
i
= 1) − (1 − v
j
)I
j
(a
E
−i
, a
i
= 0) ≤ 0 and v
j
I
j
(a
E
−{i,j}
, a
j
=
0, a
i
= 1) − v
j
I
j
(a
E
−{i,j}
, a
j
= 0, a
i
= 0) ≤ v
j
σ
2
j
. The inequality (b) follows because of the choice of
taxation t
i
. On the other hand, if a
E
i
= 1, then we must have U (a
E
−i
, a
E
i
= 1, p
a
E
) ≥ U(a
E
−i
, a
E
i
=
0, p
a
i
=0,a
E
−i
). This is a contradiction, proving the claim. Therefore, we must have a
E
≤ a
W
. We
next prove that the equilibrium is a
W
, i.e., this inequality cannot be strict. Suppose the contrary,
i.e., a
E
< a
W
is equilibrium. Using Theorem 2 we have
n
X
i=1
(1 − v
i
)I
i
(a
E
) + v
i
I
i
(a
E
−i
, a
E
i
= 0) ≥
n
X
i=1
(1 − v
i
)I
i
(a
W
) + v
i
I
i
(a
W
−i
, a
W
i
= 0). (B-26)
On the other hand, using Lemma 1 and a
E
< a
W
, we have
n
X
i=1
v
i
I
i
(a
E
−i
, a
E
i
= 0) <
n
X
i=1
v
i
I
i
(a
W
−i
, a
W
i
= 0). (B-27)
Putting (B-26) and (B-27) together, we obtain
P
n
i=1
(1 − v
i
)I
i
(a
E
) >
P
n
i=1
(1 − v
i
)I
i
(a
W
), which
contradicts the fact that a
W
is the first-best solution.
Proof of Lemma 5
Without loss of generality, suppose a
2
= · · · = a
n
= 1. We have E[X
˜
S
T
] = E[XS
T
]Σ
−1
= I. We
also have E[
˜
S
˜
S
T
] = Σ
−1
E[SS
T
]Σ
−1
= Σ
−1
(I + Σ)Σ
−1
. We first find the leaked information of user
1 if she does not share. Since, the correlation between user 1’s type and the shared data
˜
S
2
, . . . ,
˜
S
n
is zero, this leaked information is zero.
We next find the leaked information of user 1 if she shares her information. Note that
˜
S and
X
1
are jointly normal. Using the characterization of Theorem 2, this leaked information is equal to
(1, 0, . . . , 0)
Σ
−1
(I + Σ)Σ
−1
−1
(1, 0, . . . , 0)
T
= (1, 0, . . . , 0)Σ(I + Σ)
−1
Σ(1, 0, . . . , 0)
T
= (σ
2
1
, Σ
12
, . . . , Σ
1n
)(I + Σ)
−1
(σ
2
1
, Σ
12
, . . . , Σ
1n
)
T
= I
1
(a
1
= 1, a
−1
),
where the last equality follows from Theorem 2. This completes the proof of Lemma.
B-21
Proof of Theorem 11
Part 1. First note that the minimum price offered to user i to share her information with action
profile a
−i
must make her indifferent between her payoff if she shares which is given by p
i
−
v
i
I
i
(a
i
= 1, a
−1
) (where we used Lemma 5) and her payoff if she does not share which is zero.
Therefore, the minimum price offered to users i to share is v
i
I
i
(a
i
= 1, a
−i
). Since the leaked
information of users who do not share is zero, for a given action profile a ∈ {0, 1}
n
, the payoff
of the platform with minimum prices becomes
P
i: a
i
=1
I
i
(a) −
P
i: a
i
=1
p
i
=
P
i: a
i
=1
(1 − v
i
)I
i
(a).
Choosing the action profile that maximizes this payoff, completes the proof.
Part 2. Suppose a
E
is the equilibrium action profile before de-correlation. Using Lemma 3, all
low-value users share in a
E
. We have
Social surplus(a
E
) =
X
i∈V
(1 − v
i
)I
i
(a
E
) =
X
i: a
E
i
=1
(1 − v
i
)I
i
(a
E
) +
X
i: a
E
i
=0
(1 − v
i
)I
i
(a
E
)
(a)
≤
X
i: a
E
i
=1
(1 − v
i
)I
i
(a
E
)
(b)
≤ Social surplus(
˜
a
E
),
where (a) follows from the fact that for all i such that a
E
i
= 0 we must have 1 − v
i
< 0 (because all
low-value users share in equilibrium), and (b) follows because Part 1 shows that the action profile
˜
a
E
is the maximizer of
P
i: a
i
=1
(1 − v
i
)I
i
(a). Finally, note that the equilibrium social surplus after
de-correlation cannot be negative because it is equal to
P
i∈V
(1 − v
i
)
˜
I
i
(a
E
) ≥
P
i∈V
(1 − v
i
)
˜
I
i
(a =
0) = 0.
Mutual Information Satisfies Lemma 1
Monotonicity: For i ∈ V, let Y = (X
j
: a
j
= 1) and Z = (X
j
: a
0
j
= 1, a
j
= 0). Then the inequality
I
i
(a
0
) ≥ I
i
(a) becomes equivalent to
I(X
i
; Y, Z) ≥ I(X
i
; Y ).
This inequality holds because I(X
i
; Y, Z) = I(X
i
; Y ) + I(X
i
; Z|Y ) ≥ I(X
i
; Y ) where we used the
chain rule for mutual information (Theorem 2.5.2 of Cover and Thomas [2012]) and positivity of
(conditional) mutual information (Theorem 2.6.3 of Cover and Thomas [2012]).
Submodularity: For i ∈ V, let Y = (X
j
: a
j
= 1, j 6= i) and Z = (X
j
: a
0
j
= 1, a
j
= 0, j 6= i).
Then the inequality I
i
(a
i
= 1, a
−i
) − I
i
(a
i
= 0, a
−i
) ≥ I
i
(a
i
= 1, a
0
−i
) − I
i
(a
i
= 0, a
0
−i
) becomes
equivalent to
I(X
i
; X
i
, Y ) − I(X
i
; Y ) ≥ I(X
i
; X
i
, Y, Z) − I(X
i
; Y, Z).
This inequality is equivalent to I(X
i
; Y, Z) ≥ I(X
i
; Y ) which holds as we showed before.
Finally, note that if X
j
for all j such that a
j
= 1 are independent of X
i
, then I(a
i
= 0, a
−i
) =
I(X
i
, (X
j
: a
j
= 1)) = 0. Therefore, Theorem 3 (and its analogous version with competition and
B-22
unknown valuations) hold by replacing uncorrelated/correlated with independent/dependent.
More precisely, we have the following theorem:
Theorem 3 with Mutual Information 1. Suppose every high-value user is independent from
all other users. Then the equilibrium is efficient.
2. Suppose at least one high-value user is dependent (has a non-zero mutual informa-
tion) with a low-value user. Then there exists
¯
v ∈ R
|V
(h)
|
such that for v
(h)
≥
¯
v the
equilibrium is inefficient.
3. Suppose every high-value user is independent from all low-value users and at least
one high-value user is dependent with another high-value user. Let
˜
V
(h)
⊆ V
(h)
be the
subset of high-value users that are dependent with at least one other high-value user.
Then for each i ∈
˜
V
(h)
there exists ¯v
i
> 0 such that if for any i ∈
˜
V
(h)
v
i
< ¯v
i
, the
equilibrium is inefficient
B-23
