The Graph of y = ax
2
+ bx + c 393
Lesson
6-4
The Graph of
y
= ax
2
+ bx + c
Lesson 6
–
4
BIG IDEA The graph of y = ax
2
+ bx + c, a ≠ 0, is a parabola
that opens upward if a
> 0 and downward if a < 0.
Standard Form for the Equation of a Parabola
Homer King hits a high
–
fl y ball to deep center fi eld. Ignoring air
currents, which curve below most closely resembles the fl ight path
of the ball?
A B
C D
The answer is D, because high
–
fl y balls and many other projectiles
travel in parabolic paths. These paths have equations that can be put
into the standard form of a quadratic function,
y
=
ax
2
+
bx
+
c
. In
general, any equation for a parabola that can be written in the vertex
form
y
-
k
=
a
(
x
-
h
)
2
can be rewritten in the standard form
y
=
ax
2
+
bx
+
c
.
Example 1
Show that the equation y - 16 = 3(x - 5)
2
can be rewritten in the form
y = ax
2
+ bx + c, and give the values of a, b, and c.
Solution
Solve for y, then expand the binomial, distribute, and simplify.
Mental Math
Give an example of an
equation whose graph
contains (1, 3) and is
a. a line.
b. a hyperbola.
c. a parabola.
d. not a line, hyperbola, or
parabola.
Mental Math
Give an example of an
equation whose graph
contains (1, 3) and is
a. a line.
b. a hyperbola.
c. a parabola.
d. not a line, hyperbola, or
parabola.
(continued on next page)(continued on next page)
SMP_SEAA_C06L04_393-400.indd 393SMP_SEAA_C06L04_393-400.indd 393 11/19/08 2:17:24 PM11/19/08 2:17:24 PM
394 Quadratic Functions
Chapter 6
y - 16 = 3(x - 5)
2
y = 3(x - 5)
2
+ 16
Add 16 to both sides.
y = 3(x
2
- 10x + 25) + 16
Expand the binomial square.
y = 3x
2
- 30x + 75 + 16 Distribute the 3.
y = 3x
2
- 30x + 91
Arithmetic
So the original equation is equivalent to one in
standard form with a = 3, b =
–
30, and c = 91.
Check 1
Graph both y = 3(x - 5)
2
+ 16 and
y = 3x
2
- 30x + 91 on your graphng utility. Use the
trace feature and toggle between graphs to see if the
coordinates match.
The graphs seem to be identical.
Check 2
Enter the original equation into a CAS.
Add 16 to both sides of the equation.
This CAS expands the right side automatically. It checks.
QY1
In general, to change vertex form to standard form, solve for
y
and
expand.
y
-
k
=
a
(
x
-
h
)
2
y
=
a
(
x
-
h
)
2
+
k
Add
k
to each side.
y
=
a
(
x
2
- 2
hx
+
h
2
) +
k
Square the binomial.
y
=
ax
2
- 2
ahx
+
ah
2
+
k
Use the Distributive Property.
This is in standard form, with
b
=
–
2
ah
and
c
=
ah
2
+
k
. With these
substitutions, the equation becomes
y
=
ax
2
+
bx
+
c
.
Congruent Parabolas
Because the parabola determined by the equation
y
-
k
=
a
(
x
-
h
)
2
is a translation image of the parabola determined by the equation
y
=
ax
2
, the two parabolas are congruent. For all
h
and
k
,
y
–
k
=
a
(
x
-
h
)
2
can be written in standard form, so we have
the following theorem.
QY1
In Example 1, subtract the
nal expression for y from
the original expression for
y. What do you get?
QY1
In Example 1, subtract the
nal expression for y from
the original expression for
y. What do you get?
SMP_SEAA_C06L04_393-400.indd 394SMP_SEAA_C06L04_393-400.indd 394 11/19/08 2:17:28 PM11/19/08 2:17:28 PM
The Graph of y = ax
2
+ bx + c 395
Lesson 6
–
4
Parabola Congruence Theorem
The graph of the equation y = ax
2
+ bx + c is a parabola congruent
to the graph of y
= ax
2
.
Recall that a
quadratic function
is any function
f
whose equation can
be put in the form
f
(
x
) =
ax
2
+
bx
+
c
, where
a
≠ 0. Thus, the graph
of every quadratic function is a parabola, with
y
–
intercept
f
(0) =
c
.
Unless otherwise specifi ed, the domain of a quadratic function is the
set of real numbers. When
a
> 0, the range is the set of real numbers
greater than or equal to its minimum value. When
a
< 0, the range is
the set of real numbers less than or equal to its maximum value.
Applications of Quadratic Functions
Some applications of quadratic functions have been known for
centuries. In the early 17th century, Galileo described the height of
an object in free fall. Later that century, Isaac Newton derived his
laws of motion and the law of universal gravitation. In developing his
mathematical equations for the height of an object, Newton reasoned
as follows:
Gravity is a force that pulls objects near Earth downward.
Without gravity, a ball thrown upward would continue traveling
at a constant rate. Then its height would be (initial height)
+ (upward velocity) · (time). So, if it were thrown at 59 feet
per second from an initial height of 4 feet, it would continue
traveling at 59 feet per second, and its height after
t
seconds
would be 4 + 59
t
.
Galileo had shown that gravity pulls the ball downward a total
of 16
t
2
feet after
t
seconds. This effect can be subtracted from
the upward motion without gravity. Therefore, after
t
seconds,
its height in feet would be 4 + 59
t
- 16
t
2
feet. The number 16
in the expression is a constant for all objects falling at or near
Earth’s surface when the distances are measured in feet. When
measured in meters, this number is 4.9.
Example 2
A thrown ball has height h =
–
16t
2
+ 59t + 4 after t seconds.
a. Find h when t = 0, 1, 2, 3, and 4.
b. Explain what the pairs (t, h) tell you about the height of the ball for
t = 0, 2, and 4.
•
•
Sir Isaac NewtonSir Isaac Newton
(continued on next page)(continued on next page)
SMP_SEAA_C06L04_393-400.indd 395SMP_SEAA_C06L04_393-400.indd 395 11/19/08 2:18:03 PM11/19/08 2:18:03 PM
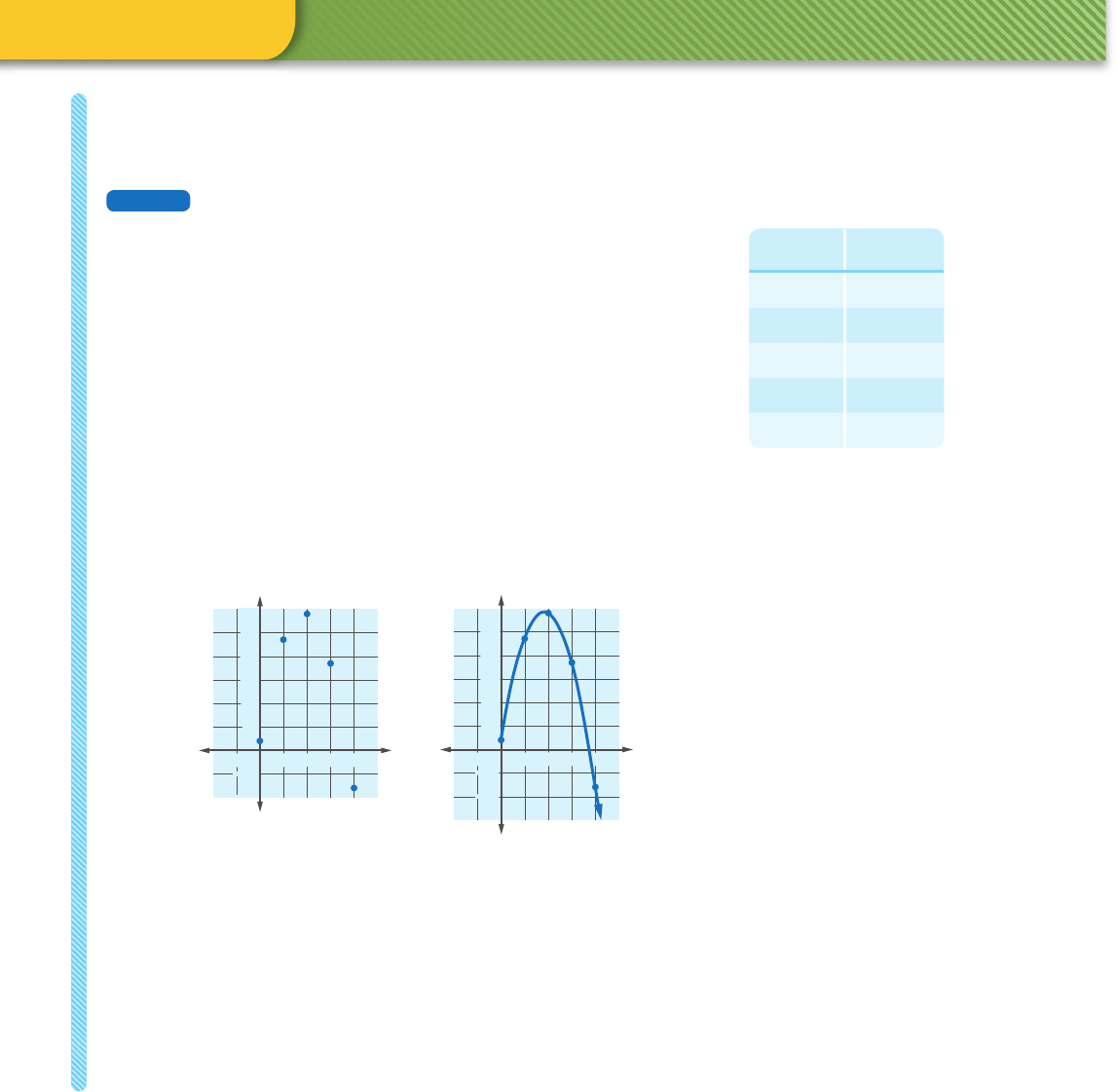
396 Quadratic Functions
Chapter 6
c. Graph the pairs (t, h) over the domain of the function.
d. Is the ball moving at the same average rate (speed) between
t = 0 and t = 1 as between t = 2 and t = 3? Justify your answer.
Solution
a. Use the table feature on your graphing utility or substitute by hand.
b. Each pair (t, h) gives the height h of the ball after t seconds.
The pair
(0, 4) means that at 0 seconds, the time of release, the ball
is 4 feet above the ground. The pair (2, 58) means the ball
is 58 feet high after 2 seconds. The pair (4, –16) means that
after 4 seconds, the ball is 16 feet below ground level. Unless
the ground is not level, it has already hit the ground.
c. The points in Part a are plotted at left below. The points do not tell much
about the shape of the graph. More points are needed to show the
parabola. By calculating h for other values of t, or by using a graphing
utility, you can obtain a graph similar to the one at the right below. The
graph is not a complete parabola because the domain of the function is
{t|t ≥ 0}.
5
321
0
4
20
30
40
50
60
᎑ 1᎑ 2
᎑ 20
h
t
10
᎑ 10
5
321
0
4
20
30
40
50
60
᎑ 2 ᎑ 1
᎑ 20
᎑ 30
᎑ 10
h
t
10
d. The average rate of change between two times is the change in height
divided by the change in time. This is the slope of the line through the
corresponding points on the graph.
The average rate of change between t = 0 and t = 1 is
47-4
_____
1-0
= 43
ft
______
second
. The average rate of change between t = 2
and t = 3 is
37-58
______
3-2
=
–
21
ft
______
second
. (The ball is moving downward
on this interval.) The rates are different, meaning the ball
travels at different speeds during its fl ight.
By the Parabola Congruence Theorem, you know that the graph of
h
=
–
16
t
2
+ 59
t
+ 4 is a translation image of the graph of
y
=
–
16
t
2
.
The equation in Example 2 is a special case of the following general
formula that Newton developed for the height
h
of an object at time
t
seconds with an initial upward velocity
v
0
and initial height
h
0
.
h
=
–
1
__
2
gt
2
+
v
0
t
+
h
0
t (sec) h (ft)
04
147
258
337
4 –16
t (sec) h (ft)
04
147
258
337
4 –16
SMP_SEAA_C06L04_393-400.indd 396SMP_SEAA_C06L04_393-400.indd 396 11/19/08 2:18:08 PM11/19/08 2:18:08 PM
The Graph of y = ax
2
+ bx + c 397
Lesson 6
–
4
In Example 2,
v
0
= 59
ft
___
sec
, the height
h
0
= 4 ft, and
g
is a constant
denoting
acceleration due to gravity
. Recall that
velocity
involves
units like miles per hour, feet per second, or meters per second.
Acceleration measures how fast the velocity changes. This “rate of
change of a rate of change” involves units like feet per second per
second (which is usually abbreviated
ft
____
sec
2
). The acceleration due
to gravity varies depending on how close the object is to the center
of a massive object. Ignoring the effects of air resistance, near the
surface of Earth,
g
≈ 32
ft
____
sec
2
, or
g
≈ 9.8
m
____
sec
2
.
Two common situations are important to note. First, if an object is
dropped, not thrown or pushed, its initial velocity
v
0
= 0. Second,
if an object starts at ground level, its initial height
h
0
= 0.
QY2
MATERIALS stopwatch, meter stick, tape, rubber ball
Work with a partner to apply Newton’s formula for free
–
falling objects.
Step 1 Copy the table below to record your data.
Initial height
h
0
(m)
Elapsed Time
Trial 1 (sec)
Elapsed Time
Trial 2 (sec)
Elapsed Time
Trial 3 (sec)
Elapsed Time
Average
t
(sec)
Partner 1
???? ?
Partner 2
???? ?
Step 2 Choose one partner to be the tosser and the other to be the
measurer. The tosser chooses a comfortable height from which to
toss the ball upward. The measurer records this height and marks
it on the meter stick with tape so the tosser can try to consistently
release the ball at the same height.
Step 3 The tosser throws the ball upward three times in succession from
the height determined in Step 2. With the stopwatch, the measurer
records the elapsed time, in seconds, from the initial release of the
ball to when it  rst hits the ground.
Step 4 Reverse roles with your partner and repeat Steps 2 and 3.
Step 5 Calculate and record average times for each partner’s tosses.
ActivityActivity
(continued on next page)(continued on next page)
SMP_SEAA_C06L04_393-400.indd 397SMP_SEAA_C06L04_393-400.indd 397 11/19/08 2:18:12 PM11/19/08 2:18:12 PM
398 Quadratic Functions
Chapter 6
Step 6 Use Newton’s formula, h =
–
1
__
2
gt
2
+ v
0
t + h
0
to calculate the initial
upward velocity v
0
for each partner’s average toss. (Hint: When did
h = 0?) Then write an equation to describe each partner’s average
toss.
Step 7 The ball reaches it maximum height in a little less than half the time
it takes the ball to hit the ground. Use your formula to estimate the
maximum height of your average toss.
Caution! The equation
h
=
–
1
__
2
gt
2
+
v
0
t
+
h
0
models the height
h
of
the object off the ground at time
t
. It
does not
describe the path of
the object. However, Galileo showed that the actual path of an object
thrown at any angle except straight up or straight down is almost
parabolic, like the path of water on the second page of the chapter,
and an equation for its path is a quadratic equation.
Questions
COVERING THE IDEAS
1.
Write the standard form for the equation of a parabola with a
vertical line of symmetry.
In 2 and 3, rewrite the equation in standard form.
2.
y
= (
x
- 3)
2
3.
y
=
–
3(
x
+ 4)
2
- 5
4. True or False For any values of
a, b,
and
c
, the graph of
y
=
ax
2
+
bx
+
c
is congruent to the graph of
y
=
ax
2
.
In 5–7, use the equation h =
–
1
__
2
gt
2
+ v
0
t + h
0
for the height of a body
in free fall.
5. Give the meaning of each variable.
a.
h
b.
g
c.
t
d.
v
0
e.
h
0
6. What value of
g
should you use if
v
0
is measured in
ft
___
sec
?
7. What is the value of
v
0
when an object is dropped?
In 8–11, refer to the graph in Example 2.
8. About how high is the ball after 1.5 seconds?
9. When the ball hits the ground, what is the value of
h
?
10. At what times will the ball be 20 feet above the ground?
11. What is the average rate of change of the ball’s height between
1 second and 3 seconds?
SMP_SEAA_C06L04_393-400.indd 398SMP_SEAA_C06L04_393-400.indd 398 11/19/08 2:18:36 PM11/19/08 2:18:36 PM
The Graph of y = ax
2
+ bx + c 399
Lesson 6
–
4
12. Suppose a person throws a ball upward at a velocity of 16
m
___
sec
from the top of a 20
–
meter tall building.
a. Write an equation to describe the height of the ball above
the ground after
t
seconds.
b. How high is the ball after 0.75 second?
c. Use a graph to estimate the ball’s maximum height.
d. After 6 seconds, is the ball above or below ground level?
Justify your answer.
APPLYING THE MATHEMATICS
13.
Sketch
y
=
–
x
2
+ 4
x
+ 6 for
–
2 ≤
x
≤ 6. On your sketch of
the graph, label the vertex and the
x
–
and
y
–
intercepts with
approximate values.
14. Consider the function
f
defi ned by the equation
f
(
x
) =
x
2
+ 3
x
- 10.
a. Sketch a graph of the function.
b. Write an equation for the line of symmetry of the parabola.
c. Estimate the coordinates of the lowest point on the parabola.
In 15 and 16, because the object is dropped, not thrown, its initial
velocity is 0.
15. Suppose a penny is dropped from the top of Taipei 101, which
in 2004 surpassed the Twin Petronas Towers in Malaysia as
the world’s tallest building. The roof of Taipei 101 is 1,474 feet
above ground.
a. Write an equation for the penny’s height as a function of time.
b. Graph your equation from Part a over an appropriate domain.
c. Estimate how much time it would take the penny to fall to
the ground.
d. When the penny falls through the atmosphere, air resistance
actually limits its velocity to a maximum of about 94 feet per
second. If the penny traveled at a constant rate of 94 feet per
second after 2.9 seconds, how much longer would it take to
reach the ground?
16. In an article about education now often circulated as a joke, the
late Dr. Alexander Calandra suggested one way to measure the
height of a building with a barometer: drop the barometer from
the top of the building and time its fall.
a. Set up an equation for the barometer’s height as a function of
time, using
h
0
for the initial height of the building.
b. Suppose it takes 3.9 seconds for the barometer to hit the
ground. Substitute values into the equation you wrote in
Part a and solve for
h
0
.
Taipei 101 in Taipei, TaiwanTaipei 101 in Taipei, Taiwan
SMP_SEAA_C06L04_393-400.indd 399SMP_SEAA_C06L04_393-400.indd 399 11/19/08 2:18:40 PM11/19/08 2:18:40 PM
400 Quadratic Functions
Chapter 6
17. Find an equation in standard form for the image of the graph of
y
=
–
1
__
4
x
2
under the translation
T
4, 2
.
REVIEW
In 18 and 19, two equations are given.
a. Graph both equations on the same set of axes.
b. Describe how the graphs of the two equations are
related.
(Lesson 6–3)
18.
y
=
x
2
and
y
= (
x
+ 3)
2
+ 4 19.
y
= 
x
and
y
- 5 = 
x
- 2
20. A gallon of paint can cover an area of 450 square feet. Find the
diameter of the largest circle that can be covered with a gallon
of paint.
(Lesson 6–2)
21. Write an inequality to describe the shaded region of the graph
at the right.
(Lessons 5–7, 3–4)
22. Solve the system
⎧
A
+
B
+
C
= 12
⎨
4
A
- 4
B
+ 2
C
=
–
16
⎩
3
A
+ 3
B
-
C
= 4
.
(Lesson 5–4)
In 23–25, nd n. (Previous Course)
23.
x
2
·
x
3
=
x
n
24.
a
n
·
a
16
=
a
64
25.
p
8
__
p
2
=
p
n
EXPLORATION
26.
How do the values of
a,
b
, and
c
affect the graph of
y
=
ax
2
+
bx
+
c
? Here are two suggested methods for
investigating:
Method 1 Use sliders on a DGS or CAS to adjust one coeffi cient,
a
,
b
, or
c
, at a time.
Method 2 a. Start with
a
= 1 and
b
= 6. Then adjust
c
and
record how the graph changes.
b. Set
a
= 1 and
c
= 4, then adjust
b
and note the
changes in the graph.
c. Set
b
= 6 and
c
= 4, then adjust
a
and note the
changes.
Is the transformation (motion) of the graph simple (like a
translation or rotation) for each change of
a
,
b
, and
c
, or is it a
compound motion? Which coeffi cients, if any, affect the graph’s
size as well as its position?
2
2
6
8
4 68
᎑ 4 ᎑ 2
᎑ 2
᎑ 4
᎑ 6
᎑ 8
y
x
4
᎑ 8 ᎑6
2
2
6
8
4 68
᎑ 4 ᎑ 2
᎑ 2
᎑ 4
᎑ 6
᎑ 8
y
x
4
᎑ 8 ᎑6
QY ANSWERS
1. 0
2. 24 ft/sec; 4 ft
SMP_SEAA_C06L04_393-400.indd 400SMP_SEAA_C06L04_393-400.indd 400 11/19/08 2:19:00 PM11/19/08 2:19:00 PM