Cheap Talk, Round Numbers, and the Economics of Negotiation

NBER WORKING PAPER SERIES

CHEAP TALK, ROUND NUMBERS, AND THE ECONOMICS OF NEGOTIATION

Matthew Backus

Tom Blake

Steven Tadelis

Working Paper 21285

http://www.nber.org/papers/w21285

NATIONAL BUREAU OF ECONOMIC RESEARCH

1050 Massachusetts Avenue

Cambridge, MA 02138

June 2015

We thank Panle Jia Barwick, Willie Fuchs, Brett Green, and Greg Lewis for helpful discussions, and

many seminar participants for helpful comments. We are grateful to Chad Syverson for sharing data

on real estate transactions in the State of Illinois. The views expressed herein are those of the authors

and do not necessarily reflect the views of the National Bureau of Economic Research. eBay Inc has

provided the data that is the basis of this study.

At least one co-author has disclosed a financial relationship of potential relevance for this research.

Further information is available online at http://www.nber.org/papers/w21285.ack

NBER working papers are circulated for discussion and comment purposes. They have not been peer-

reviewed or been subject to the review by the NBER Board of Directors that accompanies official

NBER publications.

text, not to exceed two paragraphs, may be quoted without explicit permission provided that full credit,

including © notice, is given to the source.

Cheap Talk, Round Numbers, and the Economics of Negotiation

Matthew Backus, Tom Blake, and Steven Tadelis

NBER Working Paper No. 21285

June 2015

JEL No. C78,D82,D83,M21

ABSTRACT

Can sellers credibly signal their private information to reduce frictions in negotiations? Guided by

a simple cheap-talk model, we posit that impatient sellers use round numbers to signal their willingness

to cut prices in order to sell faster, and test its implications using millions of online bargaining interactions.

Items listed at multiples of $100 receive offers that are 5% - 8% lower but that arrive 6 - 11 days sooner

than listings at neighboring "precise" values, and are 3% - 5% more likely to sell. Similar patterns

in real estate transactions suggest that round-number signaling plays a broader role in negotiations.

Matthew Backus

Department of Economics

Cornell University

Uris Hall 466

Ithaca, NY 14853

[email protected]

Tom Blake

ebay Research Labs

[email protected]

Steven Tadelis

Haas School of Business

University of California, Berkeley

545 Student Services Building

Berkeley, CA 94720

and NBER

[email protected]

1 Introduction

Bargaining is pervasive. We bargain over goods, services, salaries, real estate, territorial

boundaries, mergers and acquisitions, household chores, and more. As the Coase Theorem

demonstrates, when property rights are well-deﬁned and negotiating parties have perfect

information, bargaining leads to eﬃcient outcomes (Coase, 1960). At least since Myerson

and Satterthwaite (1983), however, economists have understood the potential for bargaining

failure. When the parties’ valuations are not commonly known, each has an incentive to

overstate the strength of their position in order to extract surplus, resulting in eﬃciency

losses. These losses can manifest in the form of delays, or the complete breakdown of

negotiations, with real economic costs. We ask whether these informational frictions can be

mitigated with the use of cheap talk, which serves as a framework for modeling negotiation.

Namely, are some market participants willing and able to signal a weak bargaining position

in order to secure a timely sale at a less advantageous price?

We take this question to a novel dataset of millions of bargaining transactions on the

eBay.com “Best Oﬀer” platform, where sellers oﬀer items at a listed price and invite buyers

to engage in alternating, sequential-oﬀer bargaining, very much in the spirit of Rubinstein

(1982). Guided by a simple model, we show that many sellers ﬁnd it beneﬁcial to signal

bargaining weakness in order to sell their items faster, albeit at lower prices.

We begin by introducing a puzzling pattern in the data. Sellers who post items

at “round-number” prices—namely multiples of $100—obtain ﬁrst-round oﬀers that are

signiﬁcantly lower than the oﬀers obtained by sellers whose posted prices are not round

numbers. This is puzzling because rather than post an item at, say $200, it seems that a

seller would be better oﬀ by choosing a lower “precise” number such as $198. And yet, such

round-number listings are very common in our setting, even among experienced sellers.

How can this be consistent with equilibrium behavior in a well-functioning marketplace

with millions of participants?

We develop a stylized model in which round numbers, such as multiples of $100, are

chosen strategically as a cheap-talk signal by impatient sellers who are willing to take a

price cut in order to sell faster. The intuition is quite simple: if round numbers are a

credible cheap-talk signal of eager (impatient) sellers, then by signaling weakness, a seller

will attract buyers faster who rationally anticipate the better deal. In equilibrium, patient

sellers prefer to hold out for a higher price, and hence have no incentive to signal weakness,

so they choose precise-number listings.

Our model yields a set of testable hypotheses that we take to the eBay data. First,

round-number listings not only attract lower oﬀers, but sell at prices that are 5%

−

8% lower

on average than nearby precise-number listings. Second, round-number listings receive

oﬀers much sooner, approximately 6 to 11 days sooner on average than precise-number

listings. Third, round-number listings are 3%

−

5% more likely to sell than precise-number

listings. These ﬁndings all support the premise of our model, that round numbers are a

cheap-talk signal used by impatient sellers. We also ﬁnd that sellers who use precise listing

prices are less likely to accept similar oﬀers than those using round listing prices, and

conditional on countering, they make more aggressive counter-oﬀers. This is consistent

with a connection between a seller’s eagerness to sell—or, formally, their private type—and

their propensity to list at round numbers.

A concern with the basic empirical ﬁndings may be that, for round-number listings,

there are unobservable diﬀerences in the seller attributes or in the products themselves,

resulting in lower oﬀers and lower prices. There are several plausible reasons this could

be the case, and such unaccounted-for heterogeneity—observable to bidders but not to

us as econometricians—can bias our estimates. We address this possibility by taking

advantage of the fact that items listed on eBay’s site in the United Kingdom (ebay.co.uk)

will sometimes appear in search results for user queries on the U.S. site (ebay.com). A

feature of the platform is that U.S. buyers who see items listed by U.K. sellers will observe

prices that are automatically converted into dollars at the contemporaneous exchange rate.

Hence, some items will be listed at round numbers in the U.K., while at the same time

appear to be precise-number listings in the U.S. Assuming that U.S. buyers perceive that

same unobserved heterogeneity as their U.K. counterparts, we can compare their behavior

to diﬀerence out the bias and demonstrate the existence of a causal eﬀect of roundness.

Another concern may be that what we ﬁnd is an artifact special to the eBay bargaining

environment. We obtain data from the Illinois real estate market that has been used by

Levitt and Syverson (2008) where we observe both the original listing price and the ﬁnal

sale price. The data does not let us perform the vast number of tests of we can for eBay’s

large data set, but we do ﬁnd evidence that homes that were listed at round numbers sell

for less than those listed at precise numbers.

Our theoretical framework is closely related to Farrell and Gibbons (1989) and Cabral

and S´akovics (1995), who show that cheap talk may inﬂuence bargaining with asymmetric

information. Single crossing in their model comes from the diﬀerential cost of bargaining

breakdown for high- and low-valuation parties.

Our single-crossing comes from diﬀerences

in patience, and we discus this and other possible mechanisms in Section 3 and 6.

Our primary contribution is empirical: we document a signaling equilibrium in the

spirit of Spence (1973) and Nelson (1974). This is challenging because the essential

components of signaling equilibria — beliefs, private information, and signaling costs

— are usually unobservable to the econometrician. The oldest thread in this literature

concerns “sheepskin eﬀects,” or the eﬀect of education credentials on employment outcomes

(Layard and Psacharopoulos, 1974; Hungerford and Solon, 1987). Regression discontinuity

has become the state of the art for estimating these eﬀects following Tyler et al. (2000), who

use state-by-state variation in the pass threshold of the GED examination to identify the

eﬀect on wages for young white men on the margin of success. By holding attributes such as

latent ability or educational inputs constant, they isolate the value of the GED certiﬁcation

itself, i.e. the pure signaling content, rather than its correlates. We complement this

literature by identifying not only the eﬀect of the signal, but also the equilibrium trade-oﬀ

that makes separating equilibrium possible in a cheap-talk setting. In this sense our

detailed data allows us to go further in proving the empirical relevance of signaling models.

Additionally, there is a small literature in empirical IO studying costly signaling games

in a variety of settings e.g. limit pricing in Gedge et al. (2013) and borrowing in Kawai

et al. (2013), as well as a growing literature on the empirics of bargaining and negotiation

(Ambrus et al., 2014; Bagwell et al., 2014; Grennan, 2013, 2014; Larsen, 2014; Shelegia

and Sherman, 2015).

Our work is also related to a literature on numerosity and cognition; in particular, how

nominal features of the action space of a game might aﬀect outcomes. Recent work in

consumer psychology and marketing has studied the use of round numbers in bargaining

(Janiszewski and Uy, 2008; Loschelder et al., 2013; Mason et al., 2013). These papers argue

from experimental and observational evidence that using round numbers in bargaining

Intuitively, high-valuation buyers (or low-valuation sellers) have more to lose from bargaining break-

down, and therefore may be willing to sacriﬁce some bargaining advantage to increase the likelihood of

transacting. Our approach is similar in that we use the probability of transacting to obtain single crossing,

but diﬀerent in that we do so by modeling the matching process of buyers to sellers. This approach is

related to a more recent literature on directed search (Menzio, 2007; Kim, 2012; Kim and Kircher, 2013)

but unlike papers in that literature we do not employ a matching function.

leads to “worse” outcomes (i.e. lower prices). By way of explanation they oﬀer an array of

biases, from anchoring to linguistic norms, and come to the brusque conclusion that round

numbers are to be avoided by the skillful negotiator.

This literature leaves unanswered

the question of why, then, as we demonstrate below, round numbers are so pervasive in

bargaining, even among experienced sellers. We reconcile these facts with an alternative

hypothesis: that round numbers are an informative signal, sometimes used to sellers’

advantage despite the negative signal they send about one’s own bargaining strength.

2 Online Bargaining and Negotiations

The eBay marketplace became famous for its use of simple auctions to facilitate trade. In

recent years, however, the share of auctions on eBay’s platform has been surpassed by

ﬁxed-price listings, many listed by businesses (Einav et al., 2013). For ﬁxed-price listings,

eBay’s platform oﬀers sellers the opportunity to sell their items using a bilateral bargaining

procedure with a feature called “Best Oﬀer”. We conjecture that, like auctions, Best Oﬀer

serves as a demand discovery mechanism for sellers.

The feature modiﬁes the listing page as demonstrated in Figure 1 by enabling the

“Make Oﬀer” button that is shown just below the “Buy It Now” button. Upon clicking the

Make Oﬀer button, a prospective buyer is prompted for an oﬀer in a standalone numerical

ﬁeld.

Submitting an oﬀer triggers an email to the seller who then has 48 hours to accept,

decline, or make a counter-oﬀer. Once the seller responds, the buyer is then sent an email

prompting to accept and checkout, make a counter-oﬀer, or move on to other items. This

feature has been growing in popularity and bargained transactions currently account for

nearly 10 percent of total transaction value in the marketplace.

From NPR (2013), Malia Mason of Mason et al. (2013) NPR interview on All Things Considered

June 3, 2013: Rob Siegel: “What do you mean don’t pick a round number?” Malia Mason: “[...] so if

you’re negotiating for, lets say, a car– you’re buying a used car from someone, [...] don’t suggest that

you’ll pay 5,000 dollars for the car. Say something like: I’ll pay you 5,225 dollars for the car, or say 4,885

dollars for the car.” Rob Siegel: “Why should that be a more successful tactic for negotiating?” Malia

Mason: “It signals that you have more knowledge about the value of the good being negotiated.”

The buyer can also send a message with their oﬀer, as seen in frame (b) of Figure 1. We leave the

analysis of those messages, which requires a diﬀerent approach, for future work.

Analyzing sellers’ choice of mechanism between auctions, ﬁxed prices, and ﬁxed prices with bargaining,

is beyond the scope of this paper. We conjecture that Best Oﬀer and auctions are alternative price

discovery mechanisms. The 30-day duration of ﬁxed price listings may be appealing when there are few

potential buyers because the 10-day maximum duration of auctions constrains its eﬀectiveness.

Figure 1: Best Oﬀer on eBay

(a) Listing Page

(b) Make an Oﬀer

Notes: Frame (a) depicts a listing with the Best Oﬀer feature enabled, which is why the “Make Oﬀer” button appears

underneath the “Buy It Now” and “Add to Cart” buttons. When a user clicks the Make Oﬀer button, a panel appears as

in frame (b), prompting an oﬀer and, if desired, an accompanying message.

Table 1: Summary Statistics

ariable Mean (Std. Dev.) N

Listing

Price (BIN) 166.478 (118.177) 10472614

Round $100 0.053 (0.225) 10472614

BIN in [99,99.99] 0.114 (0.318) 10472614

Oﬀers / Views 0.027 (0.09) 10395821

Avg First Oﬀer $ 95.612 (77.086) 2804521

Avg Oﬀer $ 105.875 (1062.989) 2804521

Avg ﬁrst Oﬀer ratio (Oﬀer/BIN) 0.631 (3.849) 2804521

Avg Counter Oﬀer 148.541 (7896.258) 1087718

Avg Sale $ 123.136 (92.438) 2088516

Search Result Hits/Day 212.718 (292.657) 10472614

Views/Day 2.093 (5.941) 10472614

Time to Oﬀer 28.153 (56.047) 2804521

Time to Sale 39.213 (67.230) 2088516

Lowest Oﬀer $ 89.107 (74.702) 2804521

Highest Oﬀer 125.06 (7381.022) 2804521

Pr(Oﬀer) 0.268 (0.443) 10472614

Pr(BIN) 0.049 (0.216) 10472614

Pr(Sale) 0.199 (0.4) 10472614

Listing Price Revised 0.570 (0.495) 4045843

# Seller’s Prior BO Listings 69974.77 (322691.987) 10472614

# Seller’s Prior Listings 87806.748 (387681.096) 10472614

# Seller’s Prior BO Threads 2451.256 (5789.343) 2804521

Notes: This table presents summary statistics for the main dataset of BO-enabled collectibles listings

created on eBay.com between June 2012 and May 2013 with BIN prices between $50 and $550.

We restrict attention to items in eBay’s Collectibles marketplace which includes coins,

antiques, toys, memorabilia, stamps, art and other like goods. Our results generalize to

other categories, but we believe that the signaling mechanism is naturally greatest in

collectibles where there is greater heterogeneity in valuations.

Our data records each bargaining oﬀer, counter-oﬀer, and transaction for any Best Oﬀer

listing. We have constructed a dataset of all single-unit Best Oﬀer enabled listings (items

for sale) that started between June 2012 and May 2013. We then limit to listings with an

initial “Buy It Now” (BIN) price between $50 and $550. This drops listings from both

sides of our sample: inexpensive listings, in which the costs of bargaining dominate the

potential surplus gains, and the right tail of very expensive listings. We are left with 10.5

million listings, of which 2.8 million received an oﬀer and 2.1 million sold.

We construct

several measures of bargaining outcomes, which are summarized in Table 1.

Note that these ﬁgures are not representative of eBay listing performance generally because we have

selected a unique set of listings that are suited to bargaining.

Figure 2: Average First Oﬀers by BIN Price

.55 .6 .65 .7 .75

Average First−Offer Ratio (Offer/Listing Price)

0 100 200 300 400 500 600

Buy It Now (Listing) Price

Round $100 Round $50 Other $ Increment

Notes: This scatterplot presents average ﬁrst oﬀers, normalized by the BIN price to be between zero and

one, grouped by unit intervals of the BIN price, deﬁned by (

z −

, z

]. When the BIN price is on an interval

rounded to a number ending in “00”, it is represented by a red circle; “50” numbers are represented by a

red triangle.

Sale prices average near 79 percent of listed prices but vary substantially. Buyers start

far more aggressively, with the average starting oﬀer at 63 percent of the posting price.

Sellers wait quite a while for (the ﬁrst) oﬀers to arrive, 28 days on average, and do not

sell for 39 days. This would be expected for items in thin markets for which the seller

would prefer a price discovery mechanism like bargaining. Finally, we also record the count

of each seller’s prior listings (with and without Best Oﬀer enabled) as a measure of the

sellers’ experience level.

To motivate the rest of the analysis, consider the scatterplot in Figure 2. On the

horizontal axis is the listing price of the goods listed for sale, and on the vertical axis we

have the average ratio of the ﬁrst oﬀer to the listed price. For example, imagine that there

were a total of three listed items at a price of $128 that received an oﬀer from some buyer.

The ﬁrst item received an oﬀer of $96, or 75% of $128, the second item received an oﬀer of

$80, or 62.5% of $128, and the third received an oﬀer of $64, or 50% of $128. The average

Figure 3: Buy it Now Prices for Best Oﬀer Listings

0 100000 200000 300000 400000 500000

Frequency

100 200 300 400 500 600

BIN Price

Notes: This is a histogram of seller’s chosen listing prices for our dataset. The bandwidth is one and unit

intervals are generated by rounding up to the nearest integer.

of these ﬁrst oﬀer ratios is

75 + 0

625 + 0

5) = 0

625

As a result, the corresponding

data point on the scatterplot would have

= 128 and

= 0

625. Because listings can be

made at the cent level, we create bins that round up the listing price to the nearest dollar

so that each listing is group into the range (

z −

, z

] for all integers

z ∈

[50

550]. That

is, a listing at $26.03 will be grouped together with a listing of $26.95, while a listing of

$24.01 will be grouped together with a listing of $25. Each point in Figure 2 represents,

at that listing price, an average across all initial buyer oﬀers for items in our sample of 2.8

million listings that received an oﬀer.

What is remarkable about this scatterplot is that when the asking price is a multiple

of $100, the average ratio of the ﬁrst oﬀer to the listed price is at least ﬁve percentage

points lower than the same average for nearby non-round listing prices. It suggests a non-

monotonicity– that sellers who list at round numbers could improve their oﬀers by either

lowering or raising their price by a small amount. However, this is not borne out by seller

behavior. We see many listings at these round numbers. Figure 3 presents a histogram

of listing prices from our dataset, showing that round numbers are disproportionately

more frequent. Moreover, as we document in Appendix H, choosing round-number

listings is prevalent even among the most experienced sellers. This observation — that

even experienced sellers seem to be selecting listing prices that elicit lower sale prices —

motivates our theoretical framework.

3 Theoretical Framework

This section presents a stylized model in which round numbers are chosen strategically

as a signal by impatient sellers who are willing to take a price cut in order to sell faster.

The intuition is quite simple: if round numbers are a credible cheap-talk signal of eager

(impatient) sellers, then by signaling weakness, a seller will attract buyers faster who

rationally anticipate the better deal. In equilibrium, patient sellers prefer to hold out for a

higher price, and hence have no incentive to signal weakness. In contrast, impatient sellers

avoid behaving like patient sellers because this will delay the sale.

The model we have constructed is deliberately simple, and substantially less general

than it could be. There are three essential components: the form of seller heterogeneity

(here, in discount rates), the source of frictions (assumptions on the arrival and decision

process), and the bargaining protocol (Nash). A very general treatment of the problem is

beyond the scope of this paper, but we appeal to the fact that there are numerous models

in the literature which share our intuition but diﬀer in the above components.

It is also important to note that we use a rather standard “non-behavioral” approach

that imposes no limits on cognition or rationality. One may be tempted to connect

roundness and precision with ideas about how limited cognition among sellers and buyers

may impact outcomes. Perhaps, a round listing price reﬂects “cluelessness” or uncertainty

about demand for the product listed. This idea is particularly compelling because it is

intuitive that sellers use the Best Oﬀer feature on eBay as a demand discovery mechanism.

If, however, round-number sellers were more uncertain about demand then they should

solicit more oﬀers and take longer to sell; instead we ﬁnd that they sell substantially sooner

With respect to seller heterogeneity, the intuition requires heterogeneity in sellers’ reserve prices.

Farrell and Gibbons (1989) impose this directly, while Menzio (2007) takes as primitive heterogeneity in

the joint surplus possible with each employer. Finally, Kim (2012) describes a market with lemons, so that

sellers have heterogeneous unobserved quality. Another critical ingredient is explaining why sellers who

oﬀer buyers less surplus in equilibrium also have non-zero market share. In a frictionless world of Bertrand

competition, this is impossible. To address this, frictions are an essential part of the model. In Farrell

and Gibbons (1989) this is accomplished by endogenous bargaining breakdown probabilities. Recent work

used matching functions to impose mechanical search frictions in order to smooth expected market shares.

All that we require of the bargaining mechanism is that outcomes depend on sellers’ private information.

Farrell and Gibbons (1989) do the general case of bargaining mechanisms, while Menzio (2007) uses a

limiting model of alternating oﬀers bargaining from Gul and Sonnenschein (1988).

than precise-number sellers. It is for this reason that we build our model on heterogeneity

in discounting rather than heterogeneity in seller informedness because the latter fails to

ﬁt the empirical facts. However, in general we acknowledge that alternative cheap-talk

signaling models could be speciﬁed with similar predictions (e.g., with heterogeneity

in seller costs)— our intention is not to sort between them, but rather to provide an

illustrative example, to derive predictions, and to use them to prove the empirical relevance

of cheap-talk signaling in bargaining.

3.1 A Simple Model of Negotiations

Consider a market in which time is continuous and buyers arrive randomly with a Poisson

arrival rate of

. Each buyer’s willingness to pay for a good is 1, and their outside option

is set at 0. Once a buyer appears in the marketplace he remains active for only an instant

of time, as he makes a decision to buy a good or leave instantaneously.

There are two types of sellers: high types (

) and low types (

), where types

are associated with the patience they have. In particular, the discount rates are

= 0

and

r >

0 for the two types, and both have a reservation value (cost) of 0 for the

good they can sell to a buyer. The utility of a seller of type

from selling his good at a

price of p after a period of time t from when he arrived in the market is e

−r

We assume that at most one

and one

type sellers can be active at any given

instant of time. If an

type seller sells his good then he is replaced immediately, so that

there is always at least one active

type seller. Instead, if an

type seller sells his good

then he is replaced randomly with a Poisson arrival rate of

. Hence, the expected time

between the departure of one

type seller and the arrival of another is

. This captures

the notion of a diverse group of sellers, where patient sellers are abundant and impatient

sellers appear less frequently.

Buyers and sellers interact in the marketplace as follows. First, upon each buyer arrival

to the marketplace, each active seller sends the buyer a cheap-talk signal “Weak” (

) or

“Strong” (

). Being cheap-talk signals, these are costless and unveriﬁable, but they may

aﬀect the buyer’s beliefs in equilibrium. Second, the buyer chooses a seller to match with.

Third and ﬁnally, upon matching with a seller, the two parties split the surplus of trade

between them given the buyer’s beliefs about the seller’s type.

For a similar continuous time matched-bargaining model see Ali et al. (2015). This split-the-surplus

“Nash bargaining” solution is deﬁned for situations of complete information, where the payoﬀ functions are

When a buyer arrives at the marketplace she observes the state of the market, which

is characterized by either one or two sellers. The assumptions on the arrival of seller types

imply that if there is only one seller, then the buyer knows that he is an

type seller,

while if there are two sellers, then the buyer knows that there is one of each type. A buyer

chooses who to “negotiate” with given her belief that is associated with the sellers’ signals.

Nash bargaining captures the idea that bargaining power will depend on the buyers’ beliefs

about whether the seller is patient (S) or impatient (W ).

We proceed to construct a separating Perfect Bayes Nash Equilibrium in which the

type chooses to reveal his weakness by selecting the signal

to negotiate a sale at a low

price once a buyer arrives, while the

type chooses the signal

and only sells if he is

alone for a high price. We verify that this is an equilibrium in the following steps.

1. High type’s price:

Let

denote the equilibrium price that a

type receives

if he choose the signal

. The

type does not care about when he sells because

his discount rate is

= 0, implying that his endogenous reservation value is

Splitting the surplus, i.e. Nash bargaining in this setting, requires that

be halfway

between that endogenous reservation value and 1, and therefore p

= 1.

2. Low type’s price:

Let

denote the equilibrium price that a

type receives from

a buyer if he chooses the signal

. If he waits instead of settling for

immediately,

then in equilibrium he will receive

from the next buyer. The Poisson arrival

rate of buyers implies that their inter-arrival time is distributed exponential with

parameter

, so the expected value of waiting is

[

−rt

], where the discount can

be solve analytically:

−rt

] =

∞

−rx

−λ

r + λ

∞

(r + λ

−x(r+λ

)

| {z }

r + λ

. (1)

common knowledge. We take the liberty of adopting the solution concept to a situation where one player

has a belief over the payoﬀ of the other player, and given that belief, the two players split the surplus.

The integral in the second line is equal to one by the deﬁnition of the exponential

distribution. Nash bargaining therefore implies

r + λ

1 ⇒ p

r + λ

2r + λ

. (2)

3. Incentive compatibility:

It is obvious that incentive compatibility holds for

types. Imagine then that the

type chooses

instead of

. Because there is always

type seller present, once a buyer arrives we assume that each seller gets to

transact with the buyer with probability

. Hence, the deviating

type either sells

= 1 or does not sell and waits for

, each with equal probability. Incentive

compatibility holds if

≥

r+λ

1, but this holds with equality from the Nash

bargaining solution that determines the L type’s equilibrium price.

3.2 Equilibrium Properties and Empirical Predictions

In equilibrium, if both sellers are present in the market then any new buyer that arrives will

select to negotiate with an

type in order to obtain the lower price of

. Furthermore,

type will sell to a buyer if and only if there is no

type seller in parallel. Because

types are replaced with a Poisson rate of

, the

type will be able to sometimes sell in

the period of time after one

type sold and another

type arrives in the market. As a

result, the equilibrium has the following properties: First, the

type sells at price

and the

type sells at price

= 1. Second, the

type sells with probability 1 to the

ﬁrst arriving buyer while the

type sells only when there is no

type. This implies a

longer waiting time for a sale for

. In turn, this implies for any given period of time, the

probability that an H type will sell is lower than that of an L type.

These equilibrium properties lend themselves immediately to several empirical predic-

tions that we can take to our data. In light of the regularity identiﬁed in Figure 2, we take

round numbers in multiples of $100 to be signals of weakness, justiﬁed further in Section

4.1. As such, the testable hypotheses of the model are as follows:

Because we use the Nash solution for the negotiation stage of the game, there is no deviation to

consider there. One could consider an alternative game in which sellers commit to a single, public signal

of their type which will be visible to all buyers. Then we should verify that the

type does not want to

deviate and commit to choose the

signal forever until he makes a sale. If the

type commits to this

strategy then his expected payoﬀ can be written recursively as

1 +

r+λ

. By analogy with (2)

this implies v = p

and so we conclude that such a deviation is not proﬁtable.

H1: Round-number listings get discounted oﬀers and sell for lower prices.

H2: Round-number listings receive oﬀers sooner and sell faster.

H3:

Round-number listings sell with a higher probability (Because listings expire, even

types may not sell).

H4: In “thick” buyer markets (higher λ

) discounts are lower.

We have chosen to model bargaining and negotiation using Nash Bargaining rather

than specifying a non-cooperative bargaining game. As Binmore et al. (1986) show, the

Nash solution can be obtained as a reduced form outcome of a non-cooperative strategic

game, most notably as variants of the Rubinstein (1982) alternating oﬀers game. Building

such a model is beyond the scope of this paper, but analyses such as those in Admati and

Perry (1987) suggest that patient bargainers will be tough and willing to suﬀer delay in

order to obtain a better price. Hence, despite the fact that within-bargaining oﬀers and

counter-oﬀers are not part of our formal model, the existing theoretical literature suggests

the following hypotheses:

H5:

Conditional on receiving an oﬀer, round-number sellers are more likely to accept

rather than counter.

H6:

Conditional on countering, round-number sellers make less aggressive counter-oﬀers.

In the above we have taken as given that round numbers are the chosen signal of

bargaining weakness. A natural question would be, why don’t impatient sellers just reduce

their listing price rather than choose a round number? In practice, sellers may be trying

to signal many dimensions of the item and their preferences simultaneously, and the level

of the price is more likely to be useful for signaling item quality to buyers. As we show

in Section 4.5 below, these signals are directing buyer search at an early stage, before

buyers are exposed to— i.e. make the investment in examining— full item descriptions or

multiple photographs. Therefore, if a seller has an item that he believes can sell for about

$70, but is willing to sell it faster at $65, then by listing it at $65 buyers may infer that it

is of lower quality and not explore the item in more detail. Instead, the round number of

$100 signals to buyers “I’m ready to cut a deal.”

4 Empirical Analysis

The goal of our empirical analysis is to test the six hypotheses using our data on Best

Oﬀer bargaining. Figure 2 is suggestive that, on average, listings at round-number prices

receive lower oﬀers than those at close-by precise-number prices. We proceed to develop

an identiﬁcation strategy based on local comparisons to estimate the magnitude of these

discontinuities in expected bargaining outcomes conditional on the listing price. This

strategy allows us to test hypotheses H1- H3.

A particular challenge is the presence of listing-level heterogeneity that may be ob-

servable to market participants but not to us. We address this problem in Section 4.3

using a sample of internationally visible listings from the ebay.co.uk website. Currency

exchange rates obfuscate roundness of the listing price seen by U.K. buyers but not by

those in the U.S., which lends itself to a diﬀerence-in-diﬀerences-style approach to show

that unaccounted-for attributes correlated with roundness do not explain our results.

In addition, we exploit detailed oﬀer-level and behavioral data to oﬀer supplementary

evidence for the signaling role of round numbers. This allows us to test hypotheses H4-H6,

as well as to identify the role of round prices in guiding buyer search, by which we can

shed some light on the signaling mechanism.

4.1 Framework and Identiﬁcation

We are interested in identifying and estimating point discontinuities in

[

|BIN price

where

is a bargaining outcome for listing

, e.g., the average ﬁrst oﬀer or the time to

the ﬁrst oﬀer. Assuming ﬁnitely many such discontinuities, z ∈ Z, we can write:

E[y

|BIN price

] = g(BIN price

) +

z∈Z

{BIN price

}β

, (3)

where

(

) is a continuous function,

is an indicator function equal to 1 if the argument

is equal to

and 0 otherwise, and

is the set of points of interest. Therefore

is the

vector of parameters we would like to estimate. Note that the set of continuous functions

(

) on

and the set of point discontinuities (

, z ∈ Z

) are mutually orthonormal; this

shape restriction, i.e. continuity of

(

), is critical to separately identify these two functions

of the same variable. However,

(

) remains an unknown, potentially very complicated

function of the BIN price, and so we remain agnostic about its form and exploit the

assumption of continuity by focusing on local comparisons. Consider two points

z ∈ Z

and (z + ∆) /∈ Z, and deﬁne the diﬀerence in their outcomes by π

(∆), i.e.:

(∆) ≡ E[y|z + ∆] − E[y|z] = g(z + ∆) − g(z) − β

. (4)

For ∆ large, this comparison is unhelpful for identifying

absent the imposition

of an arbitrary parametric structure on

(

However, as ∆

→

0, continuity implies

g(z + ∆) − g(z) → 0, oﬀering a nonparametric approach to identiﬁcation of β

= − lim

∆→0

(∆). (5)

Estimation of this limit requires estimation of

(

), which can be accomplished semi-

parametrically using sieve estimators or, more parsimoniously, by local linear regression in

the neighborhood of

. In this sense our identiﬁcation argument is fundamentally local. It

is particularly important to be ﬂexible in estimating

(

) because our theoretical framework

oﬀers no guidance as to its shape. Still, intuitively, one might suspect that it would be

monotonically increasing, and this intuition motivates an informal speciﬁcation test that

we present in Appendix A2. There we show that failing to account for discontinuities at

creates non-montonicities in a smoothed estimate of g(·).

A few remarks comparing our approach to that in regression discontinuity (RD) studies

are worthwhile. Though our identiﬁcation of

is fundamentally local, there remain two

basic diﬀerences: the ﬁrst stems from studying point rather than jump discontinuities:

where RD cannot identify treatment eﬀects for interior points (i.e., when the forcing

variable is strictly greater than the threshold), we have no such interior. Consistent with

this, we avoid the “boundary problems” of nonparametric estimation because we have

“untreated” observations on both sides of each point discontinuity. Second, RD relies

on error in assignment to the treatment group so that, in a small neighborhood of the

threshold, treatment is quasi-random. We cannot make such an argument because our

model explicitly stipulates nonrandom selection on round numbers, that sellers deliberately

and deterministically select into this group. It is therefore incumbent upon us to show

that our results are not driven by diﬀerences in unaccounted-for attributes between round-

and non-round listings, which we address in Section 4.3.

For instance, if

(

) =

αx

, then the model would be parametrically identiﬁed and estimable using

linear regression on

and

. Our results for the more ﬂexible approach described next suggest that the

globally linear ﬁt of g(·) would be a poor approximation; see Appendix C and Table A-3 in particular.

For the construction of

we have chosen to focus on round-number prices because

they appear, from the histogram in Figure 3, to be focal points. A disproportionate

number of sellers choose to use round numbers despite their apparent negative eﬀect on

bargaining outcomes. To further motivate this choice, in Appendix A4 we employ a LASSO

model selection approach to detect salient discontinuities in the expected sale price. The

LASSO model consistently and decisively selects a regression model that includes dummy

variables for the interval (

z −

, z

], where

z ∈ {

100

200

300

400

500

}

, and discards other

precise-number dummy variables.

4.2 Round Numbers and Seller Outcomes

This section implements the identiﬁcation strategy outlined above using local linear

regression in the neighborhood of

z ∈ {

100

200

300

400

500

}

to estimate

, following

the intuition of Equation (5). Our primary interest is in identifying

, and therefore

standard kernels and optimal bandwidth estimators, which are most often premised on

minimizing mean-squared error over the entire support, would be inappropriate. In order

to identify

we are interested in minimizing a mean-squared error locally, i.e. at those

points

z ∈ Z

, rather than over the entire support of

(

). This problem has been solved for

local linear regression using a rectangular kernel by Fan and Gi

jbels (1992).

Therefore

we use a rectangular kernel, which can be interpreted as a linear regression for an interval

centered at

of width 2

, where

is a bandwidth parameter that optimally depends on

local features of the data and the data-generating process. See Appendix B for the details

of the estimation of the optimal variable bandwidth.

We use separate indicators for when the BIN price is exactly a round number and

when it is “on the nines”, i.e., in the interval [

z −

, z

) for each round number

z ∈ Z

, to

account for any “left-digit” eﬀect. Therefore, conditional on our derived optimal bandwidth

and choice of rectangular kernel, we restrict attention to listings

with BIN prices

∈ [z − h

, z + h

], and use OLS to estimate:

= a

+ b

+ β

z,00

1{x

= z} + β

z,99

1{x

∈ [z − 1, z)} + 

. (6)

Imbens and Kalyanaraman (2012) extend the optimal variable bandwidth approach to allow for

discontinuities in slope as well as level. This is important in the RD setting when the researcher wants to

allow for heterogeneous treatment eﬀects which, if correlated with the forcing variable, will generate a

discontinuity in slope at jump discontinuity. We do not face this problem because we study a point rather

than a jump discontinuity, with untreated—and therefore comparable—observations on either side.

The nuisance parameters

and

capture the the local shape of

(

z,00

captures

the round-number eﬀect, and

z,99

captures any eﬀect of being listed “on the nines.” We

estimate this model separately for each z ∈ {100, 200, 300, 400, 500}.

4.2.1 Oﬀers and Prices: Testing H1

Our ﬁrst set of results concerns cases where

is the average ﬁrst buyer oﬀer and the ﬁnal

sale price of an item if sold, which tests of H1, i.e., that round-number sellers receive lower

oﬀers and settle on a lower ﬁnal sale price. Estimates for this speciﬁcation are presented

in Table 2. All results show estimates with and without eleven category-level ﬁxed eﬀects

in order to address one source of possible heterogeneity between listings.

Each cell in the table reports results for a local linear ﬁt in the neighborhood of the

round number indicated (e.g., BIN=100), using the dependent variable assigned to that

column. Table 2 reports the coeﬃcient on the indicator for whether listings were exactly

at the round number so that only

z,00

is shown. Columns 1 and 2 report estimates for all

items that receive oﬀers while Columns 3 and 4 report estimates for all items that sell,

including non-bargained sales. Results on sales are similar if the sample is restricted to

only bargained items, and remain signiﬁcant when standard errors are clustered at the

category level. We discuss results of the buyers’ choice to bargain in Appendix E.

The estimates show a strong and consistently negative relationship between the round-

ness of listed prices and both oﬀers and sales. The eﬀects are, remarkably, generally

log-linear in the BIN price, a regularity that is not imposed by our estimation procedure.

In particular, they suggest that for round BIN price listings, oﬀers and ﬁnal prices are lower

by 5%-8% as a factor of the listing price compared to their precise-number neighbors. The

estimates are slightly larger for the $500 listing value. The statistically and economically

meaningful diﬀerences in outcomes of Table 2 provide strong evidence for H1.

Ancillary coeﬃcients, i.e. the slope, and intercept of the linear approximation of

(

)

are reported and discussed in Appendix C. Importantly, we ﬁnd substantial variance in the

slope parameters at diﬀerent round numbers, which conﬁrms the importance of treating

(

) ﬂexibly. Coeﬃcients on the indicator for the “99”s, i.e. [

z −

, z

) intervals, are reported

in Appendix D. We ﬁnd that, contrary to prior work on pricing “to the nines,” in our

bargaining environment these numbers yield outcomes that are remarkably similar to those

of their round neighbors. This suggests that 99 listings also signal weakness. In Appendix

A we present estimates from a sieve estimator approach using orthogonal basis splines to

Table 2: Oﬀers and Sales for Round $100 Signals

(1) (2) (3) (4)

Avg First Oﬀer $ Avg First Oﬀer $ Avg Sale $ Avg Sale $

BIN=100 -5.372

∗∗∗

-4.283

∗∗∗

-5.579

∗∗∗

-5.002

∗∗∗

(0.118) (0.115) (0.127) (0.127)

BIN=200 -11.42

∗∗∗

-8.849

∗∗∗

-10.65

∗∗∗

-9.310

∗∗∗

(0.376) (0.369) (0.401) (0.393)

BIN=300 -18.74

∗∗∗

-14.78

∗∗∗

-17.04

∗∗∗

-15.94

∗∗∗

(0.717) (0.475) (0.863) (0.629)

BIN=400 -24.61

∗∗∗

-17.71

∗∗∗

-17.98

∗∗∗

-15.80

∗∗∗

(0.913) (0.894) (1.270) (1.186)

BIN=500 -39.43

∗∗∗

-28.58

∗∗∗

-35.76

∗∗∗

-30.55

∗∗∗

(1.320) (1.232) (1.642) (1.478)

Category FE YES YES

Notes: Each cell in the table reports the coeﬃcient on the indicator for roundness from a separate local

linear ﬁt according to Equation (6) in the neighborhood of the round number indicated for the row, using

the dependent variable shown for each column. Ancillary coeﬃcients for each ﬁt are reported in Table

A-3. Heteroskedacticity-robust standard errors are in parentheses,

∗

p < .1,

∗∗

p < .05,

∗∗∗

p < .01.

approximate

(

). Although this approach requires choosing tuning parameters (knots

and power), it has an advantage in that pooling across wider ranges of BIN prices allows

us to include seller ﬁxed eﬀects to control for seller attributes and to attempt several

speciﬁcation tests. Estimates from the cardinal basis spline approach are consistent with

those from Table 2.

4.2.2 Oﬀer Arrivals and Likelihood of Sale: Testing H2 and H3

Predictions H2 and H3 of the model are essential to demonstrate incentive compatibility

in a separating equilibrium— in particular, that round-number listings are compensated

for their lower sale price by a faster arrival of oﬀers and a higher probability of sale. To

test this in the data, we employ speciﬁcation (6) for three additional cases: where

the time to ﬁrst oﬀer, the time to sale, and the probability of sale for a listing in its ﬁrst

60 days. Results for these tests are presented in Table 3. Columns 1 and 2 show that

round-number listings receive their ﬁrst oﬀers between 6 and 11 days sooner, on an average

of about 28 days as shown in Table 1. Columns 3 and 4 show that round-number listings

also sell faster, between 10 and 14 days faster on a mean of 39 days. Hence, sellers can cut

their time on the market by up to a third when listing at round numbers. Columns 5 and

Table 3: Throughput Eﬀects of Round $100 Signals

(1) (2) (3) (4) (5) (6)

Days to Oﬀer Days to Oﬀer Days to Sale Days to Sale Pr(Sale) Pr(Sale)

BIN=100 -11.02

∗∗∗

-11.09

∗∗∗

-13.80

∗∗∗

-14.38

∗∗∗

0.0478

∗∗∗

0.0522

∗∗∗

(0.333) (0.331) (0.434) (0.432) (0.00177) (0.00176)

BIN=200 -11.53

∗∗∗

-11.52

∗∗∗

-15.15

∗∗∗

-15.64

∗∗∗

0.0550

∗∗∗

0.0590

∗∗∗

(0.526) (0.514) (0.734) (0.729) (0.00254) (0.00251)

BIN=300 -9.878

∗∗∗

-7.390

∗∗∗

-11.15

∗∗∗

-11.95

∗∗∗

0.0407

∗∗∗

0.0317

∗∗∗

(0.655) (0.384) (0.784) (0.673) (0.00303) (0.00217)

BIN=400 -7.908

∗∗∗

-6.125

∗∗∗

-10.73

∗∗∗

-10.87

∗∗∗

0.0329

∗∗∗

0.0319

∗∗∗

(0.509) (0.392) (0.849) (0.862) (0.00245) (0.00244)

BIN=500 -9.431

∗∗∗

-8.832

∗∗∗

-10.31

∗∗∗

-10.77

∗∗∗

0.0306

∗∗∗

0.0354

∗∗∗

(0.637) (0.619) (1.004) (1.009) (0.00347) (0.00348)

Category FE YES YES YES

Notes: Each cell in the table reports the coeﬃcient on the indicator for roundness from a separate local

linear ﬁt according to Equation (6) in the neighborhood of the round number indicated for the row, using

the dependent variable shown for each column. Ancillary coeﬃcients for each ﬁt are reported in Table

A-4. Heteroskedacticity-robust standard errors are in parentheses,

∗

p < .1,

∗∗

p < .05,

∗∗∗

p < .01.

6 shows that round listings also have a consistently higher probability of selling, raising

conversion by between 3 and 6 percent on a base conversion rate of 20 percent. Note

that listings may be renewed beyond 60 days, however our estimates for the eﬀect on the

probability of sale are similar when we use alternative thresholds (30, 90, or 120 days).

4.2.3 Eﬀects of Market Thickness: Testing H4

Testing H4, that “thick” markets have lower price discounts, is more challenging than the

previous three hypotheses because it requires a measure of market thickness. One could

select products that are more standardized and for which markets are likely to be thick,

compared to “long-tail” items for which markets are thin. Two drawbacks of this approach

are ﬁrst, that standardized items will have less scope for price discovery and bargaining,

A thoughtful question we have received is whether we can calculate a discount rate consistent with

our results that identiﬁes the “indiﬀerent” seller— indiﬀerent between using a round- and a nearby

precise-number listing price. In order to calculate this number we would need to make assumptions about

sellers’ costs as well as their outside option in the event of a failure to sell. We computed this estimate

under a wide array of speciﬁcations, and the resulting discount rates ranged from arbitrarily large and

negative to arbitrarily large and positive. We take from this exercise that it is impossible to learn about

the discount rate itself absent more information on the seller?s problem, however we also take that our

ﬁndings alone do not imply an unreasonably high or low discount rate.

and second, that any such selection would be ad hoc. Instead, we use behavioral data on

Search Result Page (SRP) and View Item (VI) page visits to measure market thickness.

In particular, more popular items with higher traﬃc, as measured by SRP and VI

counts can be categorized as having more buyers interested in them, and hence, thicker

markets than items with lower view counts. These items are diﬀerent in myriad other

characteristics, so we consider the results only suggestive.

The way in which traﬃc and

item popularity are measured is explained in more detail in Appendix F.

Listings are divided into deciles in increasing order of SRP and VI visit frequency. We

then replicate our local linear approach from equation (6) to estimate the eﬀect of round

listing prices on mean ﬁrst oﬀers within each decile. Figure A-3 in Appendix F plots the

point estimates and conﬁdence intervals of the discounts at round numbers. We ﬁnd lower

relative discounts for item deciles with higher view rates, which is consistent with H4. If

we use search counts as a measure of popularity, we see a U-shaped pattern where both

very low and very high search counts have lower discounts than the mid range of search

counts. Nonetheless, this relationship is still positive as suggested by H4 — a linear ﬁt of

these coeﬃcients has a signiﬁcant positive slope.

4.3 Selection on Unobservable Listing Attributes

A natural concern with the results of Section 4.2 is that there may be unaccounted-for

diﬀerences between round and non-round listings. There is substantial heterogeneity in

the quality of listed goods that is observable to buyers and sellers but controlled for in our

main speciﬁcation. This includes information in the listing title, the listing description, as

well as in the photographs. If round-number listings are of lower quality in an unobserved

way, then this would oﬀer an alternative explanation for the correlations we ﬁnd. To

formalize this idea, let the unobservable quality of a product be indexed by

with a

conditional distribution

(

ξ|BIN price

) and a conditional density

(

ξ|BIN price

). In this

light we rewrite equation (3), the expectation of y

conditional on observables, as

E[y

|BIN price

] =

g(BIN price

, ξ)dH(ξ|BIN price

) +

z∈Z

{BIN price

}β

. (7)

Our measure is an imperfect proxy for market thickness because traﬃc is only indirectly correlated

with the arrival of buyers. Perhaps quirky yet undesired items receive traﬃc because they are interesting.

From equation (7) it is clear that the original shape restriction—continuity of

(

)—is

insuﬃcient to identify

: we also require continuity of the conditional distribution of

unobserved heterogeneity in the neighborhood of each element in

. Formally, consider

the analogue of equation (5), which summarized the identiﬁcation argument from Section

4.1:

lim

∆→0

π(∆) = lim

∆→0

g(z, ξ)[h(ξ|z + ∆) − h(ξ|z)]dξ

| {z }

≡γ

−β

. (8)

The ﬁrst term on the right-hand side of equation (8), denoted

, is a potential source

of bias. Now, if we assume that the conditional distribution

(

ξ|BIN price

) is continuous

in the BIN price, then that bias is equal to zero and therefore the estimates from Section

4.2 are robust to unobserved heterogeneity. This is important: unobserved heterogeneity

alone does not threaten our identiﬁcation argument— mathematically, the concern is

discontinuities in the conditional distribution of unobserved heterogeneity. However, such

discontinuities may exist: for example, if sellers are systematically more likely to round

up than round down, then listings at round numbers will have a discontinuously lower

expected unobserved quality (

) than nearby precise listings. Moreover, a similar outcome

results if the propensity of sellers to round is correlated with

conditional on the BIN

price, e.g. if sellers of used or defective items are more likely to round. These are both

plausible stories that raise concern over the identiﬁcation argument of Section 4.2.

The ideal experiment would be to somehow hold

ﬁxed and observe the same product

listed at both round and non-round BIN prices. With observational data this is possible if

we restrict attention to well-deﬁned products, but such products will also have a well-deﬁned

market price that leaves little room for bargaining.

A similar problem arises for ﬁeld

experiments: if one were to create multiple listings for the same product, experimentally

varying roundness, they would generate their own competition. It wold be interesting,

though outside of the ambition of this paper, to construct a ﬁeld experiment with a diverse

set of listings that is large enough to make the unobserved heterogeneity average out.

Instead, here we adopt a strategy that takes advantage of the unique data already at our

disposal.

We address the problem of unobserved heterogeneity by considering a special sample

of listings that allows us to separate

, the bias term deﬁned in equation (8), and

Sellers who list on the U.K. eBay site (ebay.co.uk) enter a price in British Pounds, which

H4 suggests that in such “thick” markets, we should see little or no discount associated with roundness.

Figure 4: Example of Round UK Listing on US Site

(a) Search Results

(b) Listing Page

Notes: Frame (a) depicts a UK listing appearing in a US user’s search results; the price has converted

from British pounds into US dollars. The listing itself appears in frame (b), where the price is available in

both British pounds and US dollars.

is displayed to U.K. buyers. The sellers can choose to make their listing visible on the U.S.

site as well. U.S. buyers viewing those U.K. listings, however, observe a BIN price in U.S.

dollars as converted at a daily exchange rate. Figure 4a gives an example of how a U.S.

buyer sees an internationally cross-listed good. Because of the currency conversion, even

if the original listing price is round, the U.S. buyer will observe a non-round price when

these items appear in search results.

This motivates a new identiﬁcation strategy that is close in spirit to the “ideal”

experiment described above: For listings that are round in British Pounds, we diﬀerence

the oﬀers of U.S. and U.K. buyers. This diﬀerencing removes the common eﬀect of listing

quality (

), which is observed by both U.S. and U.K. buyers, leaving the causal eﬀect

of the round-number listing price (

). To formalize this, let

C ∈ {UK, US}

denote the

country in which the oﬀers are made, and deﬁne

We use daily exchange rates to conﬁrm that extremely few US buyers observe a round price in U.S.

dollars for U.K. listings. This sample is too small to identify a causal eﬀect of coincidental roundness.

z,C

(∆) ≡ g

(z + ∆) − g

(z) − 1{C = UK}β

. (9)

The construction in Equation (9) generalizes Equation (4) to the two-country setting.

Now, diﬀerencing π

z,U K

(∆) and π

z,U S

(∆), we obtain:

z,U K

(∆) − π

z,U S

(∆) = [g

(z + ∆) − g

(z)] − [g

(z + ∆) − g

(z)] − β

. (10)

Following the logic of the identiﬁcation argument in 4.1, we take the limit of Equation

(10) as ∆

→

0 in order to construct an estimator for

based on local comparisons. Recall

that as ∆ → 0, [g

(z + ∆) − g

(z)] → γ

so that,

= − lim

∆→0

[π

z,U K

(∆) − π

z,U S

(∆)],

which extends the identiﬁcation argument by diﬀerencing out the local structure of

(

which is common to U.K. and U.S. buyers. As in Section 4.2, we employ the results from

Fan and Gi

jbels (1992) and use a rectangular kernel with the optimal variable bandwidth;

see Appendix B for details. Then, parameters are estimated with OLS using listings with

BIN prices (denoted x

, in £) in [z − h, z + h] and oﬀers y

with the speciﬁcation:

=(a

z,U K

+ b

z,U K

(z − x

))

UK,j

z,U S

+ b

z,U S

(z − x

))

US,j

+ γ

z,00

1{x

= z} + β

z,00,U K

UK,j

1{x

= z}

+ γ

z,99

1{x

∈ (z − 1, z)} + β

z,99

UK,j

1{x

∈ (z − 1, z)} + ε

. (11)

In contrast with the estimator from Equation (6), here the unit of observation is the

buyer oﬀer. The approach is similar in spirit to a a diﬀerence-in-diﬀerences estimation

across U.S. and U.K. buyers and round- and non-round listings. In the regression,

captures the common, unobservable characteristics of the listing (observed to both U.S.

and U.K. buyers), while

is the round-number eﬀect, and is identiﬁed by the diﬀerence

in the discontinuous response of U.K. and U.S. buyers to roundness of the listing price in

British Pounds. Systematic diﬀerences between U.K. and U.S. buyers that are unrelated

to roundness, e.g. shipping costs, are captured by allowing the nuisance constant and

slope parameters to vary by the nationality of the buyer.

Table 4: Eﬀect of Roundness on Oﬀers from the UK Speciﬁcation

(1) (2)

Oﬀer $ Oﬀer $

UK x Round £100 -2.213

∗∗∗

-2.048

∗∗∗

(0.354) (0.352)

UK x Round £200 -6.409

∗∗∗

-6.386

∗∗∗

(1.000) (0.964)

UK x Round £300 -9.418

∗∗∗

-6.764

∗∗∗

(1.556) (1.413)

UK x Round £400 -16.60

∗∗∗

-18.05

∗∗∗

(2.500) (2.426)

UK x Round £500 -15.33

∗∗∗

-19.06

∗∗∗

(3.539) (3.180)

Category FE YES

Notes: Each cell in the table reports the coeﬃcient on the interaction of an indicator for roundness with an

indicator for a U.K. buyer from a separate local linear ﬁt according to Equation (11) in the neighborhood

of the round number indicated for the row, with the level of an oﬀer, either from a U.K. buyer or a U.S.

one, as the dependent variable. Heteroskedacticity-robust standard errors are in parentheses,

∗

p < .

∗∗

p < .05,

∗∗∗

p < .01.

Note that on the listing page (depicted in Figure 4b), which appears after a buyer

chooses to click on an item seen on the search results page (depicted in Figure 4a), the

original U.K. price does appear along with the price in U.S. dollars. This means that

buyers see the signal after selecting the item to place an oﬀer. The late revelation of

the signal will bias our results, but in the “right” direction because it will attenuate

any diﬀerence between U.S. and U.K. oﬀers which is a causal eﬀect of round numbers.

To the extent that we ﬁnd any causal eﬀect, we hypothesize that it survives due to the

non-salience of the U.K. price in British Pounds during the search phase of activity, and

we posit that it is a lower bound on the true causal eﬀect of the round signal.

Our sample includes all U.K.-based listings created between June 2010 and June

2013 that are internationally visible. We then take as our dependent variable all initial

oﬀers made to these listings from a U.K. or U.S. buyer. This results in a total of 2.3

million oﬀer-level observations over 600 thousand listings. In our sample we ﬁnd that U.K.

buyers tend to bid on slightly more expensive listings (£184 versus £163, on average) and

correspondingly make somewhat higher oﬀers (£113 versus £104, on average). Results

from the estimation of Equation (11) are presented in Table 4. The estimated eﬀects are

smaller than in those in Section 4.2, which could be due to either selection on unobservable

characteristics or attenuation from some U.S. buyers observing the roundness of the listing

price in British Pounds after they select to view an item. Nonetheless, the fact that the

diﬀerential response of U.S. versus U.K. bidders is systematically positive and statistically

signiﬁcant conﬁrms that our evidence for H1 cannot be fully discounted by selection on

unobservables.

4.4 Further Evidence for a Separating Equilibrium: H5 and H6

In addition to predictions for bargaining outcomes, i.e. H1-H4 from Section 3.2, our

theoretical framework also oﬀers predictions on the bargaining process based on the

separation of patient versus impatient sellers. If sellers who use precise listing prices are in

fact less patient, then we should also see that these sellers are more likely to accept a given

oﬀer (H5), and also less aggressive in their counteroﬀers (H6). To test these predictions

we take advantage of our oﬀer-level data to see whether, holding ﬁxed the level of the oﬀer,

the sellers’ type (as predicted by roundness/precision) is correlated with the probability of

acceptance or the mean counteroﬀer. Results are presented in Figure 5.

In panel 5a we plot a smoothed estimate of the probability of acceptance against the

ratio of the buyers’ ﬁrst oﬀer in a bargaining interaction to the corresponding seller’s

listing price. Normalizing by the listing price allows us to compare disparate listings and

hold constant the level of the oﬀer. We plot this for sellers who use round and precise

listing prices separately. The results show a clear and statistically signiﬁcant diﬀerence:

precise number sellers act as if they have a higher reservation price and are more likely to

reject oﬀers at any ratio of the listing price, consistent with H5.

Panel 5b plots the level of the seller’s counteroﬀer, conditional on making one, again

normalized by the listing price, against the ratio of the buyer’s oﬀer to the listing price.

Note that, unlike the results for the probability of acceptance, this sample of counteroﬀers

is selected by the seller’s decision to make a counteroﬀer at all. Again we see that precise

sellers seem to behave as if they have a higher reservation price than round sellers; their

counteroﬀers are systematically higher, consistent with H6.

It may seem surprising that oﬀers close to 100% of the list price are accepted only about half the

time. We conjecture that many sellers do not respond to the email that alerts them of an oﬀer.

Figure 5: Seller Responses to Lower Oﬀers

0 .1 .2 .3 .4 .5

Pr(Accept)

0 .2 .4 .6 .8 1

Offer / BIN

Round Precise 95% CI

(a) First Oﬀer Acceptance

.6 .7 .8 .9 1

Counter / BIN

0 .2 .4 .6 .8 1

Offer / BIN

Round Precise 95% CI

(b) Counter Oﬀer Value

Notes: Frame (a) depicts the polynomial ﬁt of the probability of acceptance for a given oﬀer (normalized by the BIN) on

items with listing prices between $85 and $115, plotted separately for $100 ‘Round’ listings and the remaining ‘Precise’

listings. Frame (b) depicts the polynomial ﬁt of the counteroﬀer (normalized by the BIN) made by a seller, similarly

constructed.

4.5 Signaling and Buyer Search Behavior

In this section we take advantage of our access to detailed data on eBay user behavior to

isolate the eﬀect of roundness as a signal on buyers’ search behavior. Our model is, like

other cheap talk models, agnostic about the form of the signal itself. Why should sellers

use roundness as a signal instead of, for instance, language in the detailed description or

a colored border on the photograph? We shed light on this by identifying the point at

which this signal aﬀects buyers’ search behavior.

In order to do this we leverage eBay’s data infrastructure to tabulate the total number

of search events that returns each listing. A search result page (SRP) contains many entries

similar to that shown in Figure 4a. We also collect the total number of times users view

the item (VI) detail page, an example of which is shown in Figure 1a. We normalize these

counts by the number of days that each listing was active to compute the exposure rate

per day for each metric. Figure 6 replicates Figure 2 for these two normalized measures

of exposure. Table 5 presents the results from a local linear estimation of the eﬀect of a

round BIN price on these two outcomes. Note that while the absolute magnitudes are

smaller in Columns (3) and (4), they are quite a bit larger relative to the average levels

that can be inferred from Figure 6. Round listings do not have a higher search exposure

rate than non-round listings, but theys have a substantially higher view-item rate.

Figure 6: Search and View Item Detail Counts

100 200 300 400 500 600

Search Result Hits/Day

0 100 200 300 400 500 600

Buy It Now (Listing) Price

Round $100 Round $50 Other $ Increment

(a) SRP Counts

1 2 3 4

Views/Day

0 100 200 300 400 500 600

Buy It Now (Listing) Price

Round $100 Round $50 Other $ Increment

(b) VI Count

Notes: This plot presents average SRP and VI events per day by unit intervals of the BIN price, deﬁned

by (

z −

, z

]. On the

axis is the BIN price of the listing, and on the

axis is the average number of

SRP arrivals per day, in panel (a), or the average number of VI arrivals per day, in panel (b). When the

BIN price is on an interval rounded to a “00” number, it is represented by a red circle; “50” numbers are

represented by a red triangle.

This is strong evidence that buyers select into round listings when seeing only infor-

mation on the search result page. That information is limited to the item title, an image

thumbnail, and the BIN price (or, currency-converted BIN price). This helps to explain

why sellers would use a price-based signal: it attracts buyers at the moment they are

looking at all similar items on the search page. There are of course, other potential signals

on the search page, but these are not cheap: the photograph conveys important information,

and Backus et al. (2014) observed that savvy sellers ﬁll the title with descriptive words

to generate SRP exposure. More importantly, however, the structure of the title and the

photograph are eBay-speciﬁc; we conjecture that roundness of the asking price is used as

a signal precisely because it is generic to bargaining marketplaces. Indeed, as we show in

the next section, there is reason to believe that roundness may be a universal signal.

5 Further Evidence from Real Estate Listings

One might wonder whether the evidence presented thus far is particular to eBay’s mar-

ketplace. Although that fact is interesting in itself, there is nothing speciﬁc to the Best

Oﬀer platform that would lead to the equilibrium we propose. There are many bargaining

settings where buyers and sellers would want to signal weakness in exchange for faster and

Table 5: Roundness and Search and View Item Detail

(1) (2) (3) (4)

SRP Hits Per Day SRP Hits Per Day VI Count Per Day VI Count Per Day

BIN=100 -40.18

∗∗∗

-23.25

∗∗∗

0.654

∗∗∗

0.703

∗∗∗

(0.640) (0.659) (0.0180) (0.0178)

BIN=200 -58.54

∗∗∗

-51.42

∗∗∗

1.005

∗∗∗

0.925

∗∗∗

(0.882) (1.042) (0.0378) (0.0365)

BIN=300 -66.59

∗∗∗

-50.42

∗∗∗

1.246

∗∗∗

0.944

∗∗∗

(1.291) (1.261) (0.0452) (0.0394)

BIN=400 -74.99

∗∗∗

-53.72

∗∗∗

1.469

∗∗∗

1.325

∗∗∗

(1.822) (1.657) (0.0540) (0.0524)

BIN=500 -95.67

∗∗∗

-82.99

∗∗∗

1.627

∗∗∗

1.384

∗∗∗

(2.100) (2.051) (0.0629) (0.0616)

Category FE YES YES

Notes: Each cell in the table reports the coeﬃcient on the indicator for roundness from a separate local

linear ﬁt according to Equation (6) in the neighborhood of the round number indicated for the row,

using the dependent variable shown for each column. Heteroskedacticity-robust standard errors are in

parentheses,

∗

p < .1,

∗∗

p < .05,

∗∗∗

p < .01.

more likely sales. We consider the real estate market as another illustration of the role

of cheap-talk signaling in bargaining. In contrast to eBay, real estate is a market with

large and substantial transactions. Sellers are often assisted by professional listing agents

making unsophisticated behavior unlikely.

We make use of the Multiple Listing Service (“MLS”) data from Levitt and Syverson

(2008) that contains listing and sales data for Illinois in from 1992 through 2002. We

consider round-number listings to be multiples of $50,000 after being rounded to the

nearest $1,000, which counts listings such as $699,950 as round. In this setting, conspicuous

precision cannot be achieved by adding a few dollars but requires a few hundred or thousand

dollars. This distinction is of little consequence since the average discount of 5% oﬀ list

still reﬂect tens of thousands of dollars. Listings bunch at round numbers, particularly

on more expensive listings, as shown in Figure 7.

Moreover, these higher value homes

which are listed at round numbers sell for lower prices that non-round listings. Figure 8

mimics Figure 2 for the real estate data using sale prices. Listings at round $50,000 sell

Recent work by Pope et al. (2014) studies round numbers as focal points in negotiated real estate

prices and argues that they must be useful in facilitating bargaining because they are disproportionately

frequent. This is consistent with our ﬁnding, documented in Appendix G, that round-number buyer oﬀers

(as opposed to public seller listing prices) signal a high willingness to pay.

Figure 7: Real Estate Grouping at round-numbers

0 .01 .02 .03 .04

Fraction

100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000

Listing Price

Notes: This is a histogram of seller’s chosen listing prices for our dataset. The bandwidth is $10,000 and

intervals are generated by rounding up to the nearest round increment (e.g., $80

000

$90

000

$100

000

, . . .

)

for less on average, which is more pronounced at the higher end of the price distribution

where there is greater clustering at round numbers.

Table 6 presents estimates from the basis spline regressions of the sale fraction on

a single dummy for whether or not the listing is round. Adding controls such as those

found in Levitt and Syverson (2008) or, as shown here, listing agent ﬁxed eﬀects, absorbs

contaminating variation in regions or home type. On average, round listings sell for 0.15%

lower than non-round listings, which represents about $600 or 3.4% of the the typical

discount oﬀ of list price.

It is interesting that the magnitude and signiﬁcance of this eﬀect

is stringer when real estate agent ﬁxed eﬀects are included, where the eﬀect is estimated

from within-agent variation. It is well known that the role of real estate agents is to help

sellers and buyers meet their objectives. Hence, if an equilibrium is played, we would

expect these expert players to play according to equilibrium. Unfortunately, we do not

observe oﬀers, unsold listings, or the time between listing and acceptance of an oﬀer, so

we are unable to test hypotheses H2-H6 in the real estate setting. Still, the fact that we

are able to replicate our ﬁnding that round numbers are correlated with lower sale prices

suggests that round-number signaling is more a general feature of real-world bargaining.

The average sales prices is 94% of the list price so sales are negotiated down 6%. For comparison, on

eBay the sales prices is 65% of list price so the eﬀect at $100 of 2% is 5.7% of the typical discount.

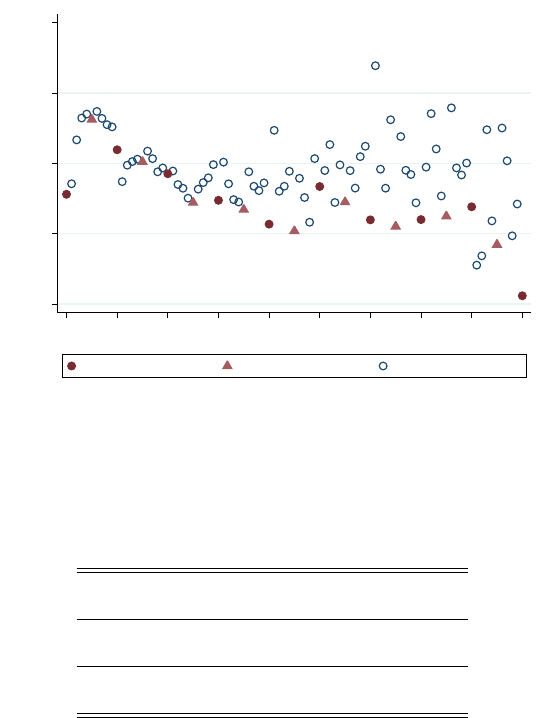
Figure 8: Real Estate Sales at Round Numbers

.94 .95 .96 .97 .98

Avg Sales Ratio (Sales Price /List Price)

100000 200000 300000 400000 500000 600000 700000 800000 900000 1000000

List Price

Round $100,000 Round $50,000 Other $10,000 Increment

Notes: This scatterplot presents average real estate sale prices in Chicago, normalized by the listing price

price to be between zero and one, grouped by $10,000 intervals of the listing price, When the listing price

is on an interval rounded to the hundreds of thousands, it is represented by a red circle; numbers rounded

to ﬁfty thousands are represented by a red triangle.

Table 6: Real Estate Basis Spline Estimates

(1) (2)

Sale $ / List $ Sale $ / List $

Round $50k -0.000956 -0.00145

∗∗

(0.000652) (0.000696)

Agent FE YES

N 35808 35808

Notes: Here we report coeﬃcients on a regression form of (3) where

is real estate sale prices in Chicago,

(

) is approximated using a cardinal basis spline, and the coeﬃcient of interest is on a dummy for the

listing price of a home being rounded up to a multiple of $50,000.

6 Discussion

This study began with an empirical observation that eBay sellers who list goods at

round numbers with the Best Oﬀer mechanism received substantially lower oﬀers and

ﬁnal proceeds than sellers using more precise numbers in the same price range. We

identiﬁed this eﬀect nonparametrically and carefully demonstrated that it is not explained

by unobserved diﬀerences in item or seller attributes. Our main contribution, however,

is an explanation for the eﬀect. We found strong evidence of behavior consistent with

a cheap-talk signaling equilibrium where round-number listings elicit lower oﬀers with a

higher probability of a successful sale and less time on the market than similar precise-

number listings. Moreover, we were able to show that subsequent seller behavior was

consistent with that cheap-talk signaling interpretation– sellers who use precise-number

listing prices went on to bargain more aggressively, while sellers who used round numbers

were more likely to settle and made less aggressive counter-oﬀers. The narrative behind

our approach is one of sophisticated equilibrium behavior in which buyers and sellers are

aware of the features and codes of an intricate separating equilibrium of a cheap-talk game.

As we have demonstrated, the data are consistent with equilibrium behavior across many

dimensions.

Other work on round numbers has focused on behavioral explanations, most notably

Lacetera et al. (2012) who conjecture that the way buyers respond to round numbers is

consistent with left-digit inattention, a form of bounded rationality. We don’t believe that

stories of bounded or partial rationality would easily explain the empirical ﬁndings of our

study. In particular, as we show in Appendix D, there is no discontinuity of the left-digit

bias type. In fact, the $99 signal (including anything from $99 to $99.99) seems to be

equivalent to the $100 signal. Perhaps, there is no tension between our results and those of

Lacetera et al. (2012) because their variable of interest is a vehicle’s mileage, which is an

exogenous characteristic of the item, while ours is the listing price, which is an endogenous

signal chosen by the seller. We also note that we ﬁnd price eﬀects four to ﬁve times larger

than theirs, which suggests that an alternative mechanism is at play.

One form of bounded rationality that seems appealing that sellers who are clueless

about the item they are selling use round numbers because they are inattentive. Buyers

thus target these clueless sellers with lower oﬀers. If these clueless sellers are also more

eager to sell, it would explain why round-number items would sell faster. There are

several reasons that we ﬁnd this story unappealing. First, why would the inattentive

sellers systematically choose round numbers that are signiﬁcantly higher than the ﬁnal

price? If their mistakes are equally likely to be both under- and over-estimates of the

items they are selling, then competitive pressure would push under-estimated items to sell

above the listed price. Second, if they are clueless, but rationally so, then they should

try to collect more signals about the value of the item, thus waiting at least as long as

others, if not longer, to sell their items. It seems therefore unlikely that clueless sellers

would also be impatient. Finally, our data shows that even the most experienced sellers

use round-number listings quite often, suggesting that this behavior is not likely to be

a consistent mistake (see Appendix H). Though we acknowledge the intuitive appeal of

the story, we conjecture that seller cluelessness is a correlate being in a weak bargaining

position, rather than the primitive.

The fact that we ﬁnd some supporting evidence from the real-estate market further

strengthens our conclusion that round numbers play a signaling role in bargaining situations.

People have used one form or another of bargaining for millennia. We don’t believe that

all people are literally playing a sophisticated Perfect-Bayesian equilibrium of a complex

game; rather, we believe that they are playing as if they were. In other words, even if

the mechanical truth is that there are cognitive heuristics or social norms behind our

interpretation of the roundness and precision of numbers, the question then becomes why

those heuristics or norms persist. We conjecture that they persist precisely because they

are consistent with equilibrium play in a rational expectations model— that, in equilibrium,

they are unbiased and create no incentive to deviate.

If this is indeed the case, it suggests

that over time, players ﬁnd rather sophisticated, if not always intuitive, ways to enhance

the eﬃciency of bargaining outcomes in situations with incomplete information.

Experimental evidence inThomas et al. (2010) demonstrates the plasticity of perceptual biases

associated with roundness.

References

Admati, A. and Perry, M. (1987). Strategic delay in bargaining. Review of Economic Studies, 54(3):345–364.

Ali, S. N., Chen-Zion, A., and Lillethun, E. (2015). A networked market for information. Working Paper.

Ambrus, A., Chaney, E., and Salitskiy, I. (2014). Pirates of the mediterranean: An empirical investigation

of bargaining with asymmetric information. Working Paper.

Backus, M., Podwol, J., and Schneider, H. (2014). Search costs and equilibrium price dispersion in auction

markets. European Economic Review, 71:173–192.

Bagwell, K., Staiger, R., and Yurukoglu, A. (2014). Multilateral trade bargaining:A ﬁrst peek at the

GATT bargaining records. Working Paper.

Binmore, K., Rubinstein, A., and Wolinsky, A. (1986). The nash bargaining solution in economic modelling.

RAND Journal of Economics, 17(2):176–188.

Cabral, L. and S´akovics, J. (1995). Must sell. Journal of Econoomics and Management Strategy, 4(1):55–68.

Coase, R. J. (1960). The problem of social cost. Journal of Law and Economics, 3:1–44.

De Boor, C. (1978). A practical guide to splines. Number 27 in Applied Mathematical Sciences, volume 27

of Applied Mathematical Sciences. Springer, New York.

DesJardins, S. L. and McCall, B. P. (2008). The impact of the gates millennium scholars program on the

retention, college ﬁnance- and work-related choices, and future educational aspirations of low-income

minority students. Working Paper.

Dierckx, P. (1993). Curve and surface ﬁtting with splines. Oxford University Press, Inc.

Einav, L., Farronato, C., Levin, J. D., and Sundaresan, N. (2013). Sales mechanisms in online markets:

What happened to internet auctions? NBER Working Paper.

Fan, J. and Gi

jbels, I. (1992). Variable bandwidth and local linear regression smoothers. The Annals of

Statistics, 20(4):2008–2036.

Farrell, J. and Gibbons, R. (1989). Cheap talk can matter in bargaining. Journal of Economic Theory,

48(1):221–237.

Gedge, C., Roberts, J. W., and Sweeting, A. (2013). A model of dynamic limit pricing with an application

to the airline industry. Working Paper.

Grennan, M. (2013). Price discrimination and bargaining: Empirical evidence from medical devices.

American Economic Review, 103(1):145–177.

Grennan, M. (2014). Bargaining ability and competitive advantage: Empirical evidence from medical

devices. Management Science, 60:3011–3025.

Gul, F. and Sonnenschein, H. (1988). On delay in bargaining with one-sided uncertainty. Econometrica,

56:601–611.

Hungerford, T. and Solon, G. (1987). Sheepskin eﬀects in the return to education. The Review of

Economics and Statistics, 69(1):175–178.

Imbens, G. and Kalyanaraman, K. (2012). Optimal bandwidth choice for the regression discontinuity

estimator. Review of Economic Studies, 79(3):933–959.

Janiszewski, C. and Uy, D. (2008). Precision of the anchor inﬂuences the amount of adjustment.

Psychological Science, 19(2):121–127.

Kawai, K., Onishi, K., and Uetake, K. (2013). Signaling in online credit markets. Working Paper.

Kim, K. (2012). Endogenous market segmentation for lemons. RAND Journal of Economics, 43(3):562–576.

Kim, K. and Kircher, P. (2013). Eﬃcient competition through cheap talk: Competing auctions and

competitive search without ex ante price commitment. WorkingPaper.

Lacetera, N., Pope, D., and Sydnor, J. (2012). Heuristic thinking and limited attention in the car market.

American Economic Review, 102(5):2206–2236.

Larsen, B. (2014). The eﬃciency of real-world bargaining: Evidence from wholesale used-auto auctions.

NBER Working Paper No. 20431.

Layard, R. and Psacharopoulos, G. (1974). The screening hypothesis and the returns to education. Journal

of Political Economy, 82:985–998.

Levitt, S. D. and Syverson, C. (2008). Market distortions when agents are better informed: The value of

information in real estate transactions. The Review of Economics and Statistics, 90(4):599–611.

Loschelder, D., Stuppi, J., and Tr¨otschel, R. (2013). “

14,875?!”: Precision boosts the anchoring potency

of ﬁrst oﬀers. Social Psychological and Personality Science, pages 1–9.

Mason, M., Lee, A., Wiley, E., and Ames, D. (2013). Precise oﬀers are potent anchors: Conciliatory

counteroﬀers and attributions of knowledge in negotiations. Journal of Experimental Social Psychology,

49:759–763.

Menzio, G. (2007). A theory of partially directed search. Journal of Political Economy, 115(5):748–769.

Myerson, R. B. and Satterthwaite, M. A. (1983). Eﬃcient mechanisms for bilateral trading. Journal of

economic theory, 29(2):265–281.

Nelson, P. (1974). Advertising as information. Journal of Political Economy, 82(4):729–754.

NPR (2013). Next time you ask for a raise, you might want to round up.

Pope, D. G., Pope, J. C., and Sydnor, J. R. (2014). Focal points and bargaining in housing markets.

Working Paper.

Rubinstein, A. (1982). Perfect equilibrium in a bargaining model. Econometrica, 50(1):97–110.

Shelegia, S. and Sherman, J. (2015). When the price you see is not the price you get: A ﬁeld study.

Working Paper.

Spence, M. (1973). Job market signaling. Quarterly Journal of Economics, 87(3):355–374.

Thomas, M., Simon, D., and Kadiyali, V. (2010). The price precision eﬀect: Evidence from laboratory

and market data. Marketing Science, 29(1):175–190.

Tyler, J. H., Murnane, R. J., and Willett, J. B. (2000). Estimating the labor market signaling value of

the ged. Quarterly Journal of Economics, 115(2):431–468.

Appendices

A Alternative Approach: Basis Splines

1 Basis Splines

Our main results from Section 4.2 employ a local linear speciﬁcation that identiﬁes

(

)

from equation (3) only in small neighborhoods of the discontinuities we study. There are

a number of additional questions we could ask with a more global estimate of

(

): for

instance, one might be interested in the shape of

(

), or in using all of the data for the

sake of estimating seller ﬁxed eﬀects as we do in Section A3. To this end we employ a

cardinal basis spline approximation (De Boor, 1978; Dierckx, 1993), a semi-parametric

tool for ﬂexibly estimating continuous functions. Intuitively, a cardinal basis spline is a

set of functions that form a linear basis for the full set of splines of some order

on a

ﬁxed set of knots. This is a convenient framework because the weights on the components

of that linear basis can be estimated using OLS, which will identify the spline that best

approximates the underlying function.

The approach requires that we pick a set of

equidistant “knots”, indexed by

, which

partition the domain of a continuous one-dimensional function of interest

(

) into segments

of equal length.

We also select a power

, which represents the order of diﬀerentiability

one hopes to approximate. So, for instance, if

= 2 then one implements a quadratic

cardinal basis spline. Given a set of knots and

, cardinal basis spline functions

j,p

(

)

are constructed recursively by starting at power p = 0:

j,0

(x) =







1 if t

≤ x < t

j+1

0 else

, (1)

and

j,p

(x) =

x − t

j+p−1

− t

j,p−1

(x) +

j+p

− x

j+p

− t

j+1

j+1,p−1

(x). (2)

The fact that knots are equidistant is what makes this a cardinal, rather than an ordinary basis spline.

In principle, one could pick the knots many diﬀerent ways.

Appendix-1

Given a set of cardinal basis spline functions

≡ {B

j,p

}

j=1...k+p

, we construct the

basis spline approximation as:

f(x) '

j=1,...,k

j,p

(x), (3)

where the vector α is chosen by OLS.

An advantage of the cardinal basis spline approach is that, for appropriately chosen

any spline of order

on that same set of knots can be constructed as a linear combination

of the elements of

. Therefore we can appeal to standard approximation arguments for

splines to think about the asymptotic approximation error as the number of knots goes to

inﬁnity.

2 Identiﬁcation Argument with Basis Splines

Here we present additional, albeit less formal evidence for our identiﬁcation strategy. We be-

gin with the premise — an intuitive assertion — that one would expect

[

sale price|BIN price

]

to be monotonically increasing in the BIN price. This is testable insofar as we can estimate

(

) over large regions of the domain— we therefore employ the cardinal basis spline

approach of Appendix 1 to estimate this expectation in the neighborhood of BIN prices

near 500, without including dummies for round numbers. Predicted values from this

regression are presented in Figure A-1a. One notes the counter-intuitive non-monotonicity

in the neighborhood of 500; contrary to the premise with which we began, it appears that

the derivative of

(

) is locally negative. This phenomenon can be documented near other

round numbers as well.

To resolve this surprising outcome, it is suﬃcient to re-run the regression with dummies

for

{

[499

500)

500

}

. Predicted values from the regression with dummies are presented

in Figure A-1b, which conﬁrms that the source of the non-monotonicity was the behavior

of listings at those points. We take this as informal evidence for the claim that a model of

[

sale price|BIN price

] should allow for discontinuities at round numbers; that something

other than the level of the price is being signaled at those points.

Appendix-2

Figure A-1: Basis Spline Identiﬁcation

300 350 400 450

Sale Price

490 500 510

BIN Price

(a) No Dummy

300 350 400 450

Sale Price

490 500 510

BIN Price

(b) With Dummy

Notes: This ﬁgure depicts a cardinal basis spline approximation of E[sale price|BIN price] without (a) and with (b) indicator

functions 1{BIN ∈ [499, 500)} and 1{BIN = 500}. Sample was drawn from collectibles listings that ended in a sale using

the Best Oﬀer functionality.

3 Basis Spline Robustness

An additional beneﬁt of estimating

(

) globally, as the basis spline approach of Appendix

1 allows, is that we are able to employ the full dataset of listings and oﬀers. This permits

the estimation of seller-level ﬁxed eﬀects, which is important because they address any

variation of a concern in which persistent seller-level heterogeneity drives our results. This

is an extension of the local linear speciﬁcation because it permits the use of all of listings

simultaneously and not just those observations local to the threshold. That adds many

observations per seller to each regression, some round and some non-round, identifying the

eﬀect within seller. Table A-1 shows the breakdown, by listing count, of the percentage

of sellers that have a mix of both round and non-round listings. In general, we ﬁnd that

propensity to list round declines with experience (See Table A-8) and that ﬁrst listings are

more likely to be round than later listings. Yet even very large sellers use round numbers

for some of their listings. For instance, 43 percent of sellers with 10 or more listings (19

percent of all sellers) have some mix of round and non-round listings, allowing for the

identiﬁcation of the sample.

Moreover, as shown in Table A-8, 22 percent of listings by the top decile of sellers are round.

Appendix-3

Table A-1: Within Seller Variation of Roundness

% Split Count

1 Listing 0.00 99637

2-5 Listings 0.19 114609

6-9 Listings 0.32 35304

>=10 Listings 0.46 86445

Notes: Here we summarize the extent to which sellers, categorized by the number of listings they have

generated, mix between round- and non-round listing prices, where roundness is deﬁned by the use of an

exact “00” number.

Table A-2 presents results with and without seller-level ﬁxed eﬀects for the average

ﬁrst oﬀer as well as the sale price. These results are consistent with those from Table

2, which rules out most plausible stories of unobserved heterogeneity as an alternative

explanation for our ﬁndings.

Table A-2: Basis Splines Estimation for Oﬀers and Sales for Round $100

Signals

(1) (2) (3) (4)

Avg First Oﬀer $ Avg First Oﬀer $ Avg Sale $ Avg Sale $

BIN=100 -4.835

∗∗∗

-1.189

∗∗∗

-4.396

∗∗∗

-2.080

∗∗∗

(0.292) (0.288) (0.304) (0.290)

BIN=200 -8.863

∗∗∗

-4.804

∗∗∗

-6.609

∗∗∗

-5.266

∗∗∗

(0.456) (0.443) (0.488) (0.459)

BIN=300 -14.37

∗∗∗

-8.781

∗∗∗

-12.10

∗∗∗

-8.797

∗∗∗

(0.602) (0.584) (0.674) (0.634)

BIN=400 -16.94

∗∗∗

-12.12

∗∗∗

-13.91

∗∗∗

-12.47

∗∗∗

(0.734) (0.714) (0.843) (0.795)

BIN=500 -31.02

∗∗∗

-23.97

∗∗∗

-33.59

∗∗∗

-27.30

∗∗∗

(0.870) (0.851) (1.042) (0.985)

Category FE Yes Yes

Seller FE Yes Yes

N 2804521 2804521 1775014 1775014

Notes: Here we report coeﬃcients on a regression form of (3) where

is average ﬁrst oﬀers and sale

prices and g(·) is approximated using a cardinal basis spline.

4 LASSO Model Selection

We also employ the cardinal basis spline approach to oﬀer supplementary motivation for

our choice of the set of discontinuties

. Based on the size of our dataset it is tempting to

Appendix-4

suppose that approximation error in

would yield evidence of discontinuities at any point,

and therefore it is non-obvious that we should restrict attention to round numbers. To

answer this concern we use LASSO model selection to construct

. We include dummies for

dBIN pricee

for all integers in the window [

k −

, k

+ 25] for

k ∈ {

100

200

300

400

500

}

These integers are constructed in similar fashion as the buckets used for Figure 2, where

every listing is included and the dummy indicates whether the listing is in the range

(

n −

, n

] for all integers in the range [

k −

, k

+ 25]. We then include every dummy as

well a continuous approximation to

(

) so that the LASSO optimization problem is as

follows:

min

j=1,...,N

−

s∈S

(x) +

z∈Z

{BIN price

}

− λ

z∈Z

|β

| (4)

Note that we do not penalize the LASSO for using the cardinal basis spline series

(

) to

ﬁt the underlying

(

). In this sense we are considering the minimal set of deviations from

a continuous estimator. Figure A-2 presents results. On the x axis is

log

(

λ/n

), and on the

y axis is the coeﬃcient value subject to shrinkage. What is striking about these ﬁgures

is that the coeﬃcient

x00

(shown in red) is salient relative to other discontinuities, even

when the penalty term is large, and this pattern holds true for all ﬁve of the neighborhoods

we study.

B Bandwidth

We implement the optimal bandwidth selection proposed by Fan and Gi

jbels (1992) and

described in detail by DesJardins and McCall (2008) and Imbens and Kalyanaraman

(2012). We estimate the curvature of

(

) and the variance in a broad neighborhood of

each multiple of $100, which we arbitrarily chose to be +/- $25. We then compute the

bandwidth to be (

)

(

× | ˜g

(100

∗ i

)

−

where

i ∈

5]. We estimate

using

the standard deviation of the data within the broad neighborhood of the discontinuity.

We estimate

˜g

(

) by regressing the outcome on a 5th order polynomial approximation of

and analytically deriving ˜g

(·) from the estimated coeﬃcients.

Appendix-5

Figure A-2: LASSO Model Selection

(a) $100

0.00 0.05 0.10 0.15 0.20

−5 0 5

(b) $200

0.0 0.1 0.2 0.3

−10 −5 0 5 10 15

0.0 0.1 0.2 0.3 0.4 0.5

−20 −15 −10 −5 0 5 10 15

(d) $400

0.0 0.1 0.2 0.3 0.4

−30 −20 −10 0 10 20 30

(e) $500

0.0 0.1 0.2 0.3 0.4 0.5 0.6

−150 −100 −50 0 50

Plots show coeﬃcients (vertical axis) for varying levels of λ in the Lasso where the dependent variable of sale price and

regressors are dummies for every dollar increment between -$25 and +$25 of each $100 threshold. The red lines represent

each plots respective round $100 coeﬃcient. The Lasso includes unpenalized basis spline coeﬃcients (not shown).

C Local Linear Ancillary Coeﬃcients

Table A-3 presents ancillary coeﬃcients for the local linear regression results for Table

2. The BIN price variable is re-centered at the round number of interest, so that the

constant coeﬃcient can be interpreted as the value of

(

) locally at that point. The slope

coeﬃcients deviate substantially from what one might expect for a globally linear ﬁt of

the scatterplot in Figure 2 (i.e., roughly 0

65). In other words, it seems that the function

g(·) exhibits substantial local curvature, which oﬀers strong supplemental motivation for

Appendix-6

being as ﬂexible and nonparametric as possible in its estimation. Similarly, Table A-4

presents ancillary coeﬃcients corresponding to our local linear throughput results in Table

3. Optimal bandwidth choices for both tables reﬂect the fact that there is more data

available for lower BIN prices.

D The 99 eﬀect

The regressions of Section 4.2 included indicators

1{BIN price

as well as indicators

1{BIN price

∈

[

z −

, z

)

}

for

z ∈ {

100

200

300

400

500

}

. Table A-5 reports the coeﬃ-

cients on the latter indicators, which capture the eﬀect of pricing “to the nines”. Perhaps

surprisingly, the results are very similar to those in Table 2; it seems that listing prices

of $99.99 and $100 have the same eﬀect relative to, for instance, $100.24. We take this

as evidence that the left-digit inattention hypothesis does not explain our ﬁndings. It

suggests that what makes a “round” number round, for our purposes, is not any feature

of the number itself but rather convention — a Schelling point — consistent with our

interpretation of roundness as cheap talk.

This ﬁnding also suggests that we can pool the signals, letting

{

[99

100]

[199

200]

[299

300]

[399

400]

[499

500]

}

. Results for that regression are reported in Table A-6.

Consistent with our hypothesis, this does not substantively alter the results.

E Non-Bargained Transactions

Our model does not incorporate any costs of bargaining or the option to pay the advertised

listing price. In reality buyers choose between paying full price and engaging in negotiation.

On eBay, the former is done by clicking the “Buy-It-Now” button and immediately checking

out. Though this is outside of our model, it is intuitive that when there is more surplus

to be had from negotiation, i.e. when the seller uses a round listing price, buyers will be

relatively less likely to exercise the Buy-it-Now option. In order to test this, we employ

our local linear speciﬁcation from Equation (6) to predict the likelihood that the a listing

sells at the BIN price and, secondarily, the likelihood that a listing sells at the BIN price

conditional on a sale.

Results are presented in Table A-7. Somewhat counter-intuitively, columns (1) and

(2) suggest that round-number listings are more likely to sell at the BIN price than

Appendix-7

Table A-3: Intercepts and Slopes for Each Local Linear Regression

(1) (2) (3) (4)

Avg First Oﬀer $ Avg First Oﬀer $ Avg Sale $ Avg Sale $

Near round $100:

Constant 60.17

∗∗∗

61.38

∗∗∗

82.26

∗∗∗

79.67

∗∗∗

(0.0861) (0.168) (0.0902) (0.178)

Slope 0.654

∗∗∗

0.687

∗∗∗

1.088

∗∗∗

1.074

∗∗∗

(0.0184) (0.0173) (0.0181) (0.0181)

Bandwidth 6.441 7.388 7.615 7.492

N 286606 289772 224868 224445

Near round $200:

Constant 119.2

∗∗∗

120.0

∗∗∗

162.8

∗∗∗

156.3

∗∗∗

(0.314) (0.467) (0.322) (0.503)

Slope 0.928

∗∗∗

1.006

∗∗∗

1.762

∗∗∗

1.592

∗∗∗

(0.0639) (0.0622) (0.0674) (0.0655)

Bandwidth 8.171 8.253 7.365 7.662

N 151004 151093 103690 103898

Near round $300:

Constant 175.5

∗∗∗

172.2

∗∗∗

242.9

∗∗∗

232.1

∗∗∗

(0.609) (0.586) (0.735) (0.756)

Slope 1.416

∗∗∗

0.737

∗∗∗

2.156

∗∗∗

1.408

∗∗∗

(0.118) (0.0210) (0.149) (0.0605)

Bandwidth 9.985 22.46 8.595 12.73

N 101690 137956 63270 70069

Near round $400:

Constant 231.6

∗∗∗

222.1

∗∗∗

322.4

∗∗∗

303.5

∗∗∗

(0.660) (1.058) (1.020) (1.335)

Slope 1.406

∗∗∗

1.234

∗∗∗

2.111

∗∗∗

1.763

∗∗∗

(0.0742) (0.0690) (0.146) (0.128)

Bandwidth 16.03 17.97 12.55 14.20

N 80967 81413 44154 44443

Near round $500:

Constant 279.7

∗∗∗

275.7

∗∗∗

396.8

∗∗∗

376.7

∗∗∗

(1.065) (1.432) (1.276) (1.641)

Slope 1.433

∗∗∗

1.457

∗∗∗

2.712

∗∗∗

1.748

∗∗∗

(0.131) (0.110) (0.216) (0.141)

Bandwidth 16.62 19.48 14.22 16.29

N 69129 69615 36003 37201

Category FE YES YES

Standard errors in parentheses

∗

p < .1,

∗∗

p < .05,

∗∗∗

p < .01

Notes: Here we report ancillary coeﬃcients from separate local linear ﬁts according to Equation (6) in the

neighborhood of the round number indicated for the row, using the dependent variable shown for each

column, corresponding to Table 2. Heteroskedacticity-robust standard errors are in parentheses,

∗

p < .

∗∗

p < .05,

∗∗∗

p < .01.

Appendix-8

precise-number listings. However, this derives from the fact that round-number listings

enjoy heavier buyer traﬃc, as we have documented in Tables 3 and 5. When we condition

on sale, as we do in columns (3) and (4), for the elements of

where we have the most

observations we see a large and negative eﬀect consistent with our intuition— that buyers

are more likely to engage in negotiation conditional on purchasing from a round- rather

than a precise-number seller. In other words, buyers’ decisions about when to engage in

negotiation are consistent with beliefs implied by our model.

F Hypothesis H4

An ancillary prediction of the model is that “thick” markets will have lower discounts

than thinner markets. Low type (inpatient) sellers do not have to wait as long for buyers

in thicker markets so they do not have to oﬀer as deep discounts to rationalize signaling

weakness. We take this to the data by conjecturing that thicker markets will have more

traﬃc (views and search events) for items in thicker markets. This is an imperfect proxy

since traﬃc is only indirectly correlated with the arrival of actual buyers.

We proceed by grouping listings into deciles by view item counts. We ﬁrst ﬁnd that

the baseline (non-round) mean oﬀers vary across decile of exposure. This is an undesired

byproduct of group by exposure: items in these groupings are diﬀerent in ways other

than pure buyer arrival rates (

). We correct for this by normalizing estimates by the

baseline mean oﬀer. That is, we normalize

by the constant

in Equation 6. Otherwise,

estimation proceeds just as in Equation 6, but separately for each decile of exposure.

Figure A-3 shows the results. This ﬁgure plots the point estimates and conﬁdence

interval of the local linear estimation of the round-number BIN eﬀect on mean ﬁrst oﬀers

for each decile of view item detail counts and search result exposure counts. The x-axis

shows the decile for each viewability metric, with 10 being have the highest search and

item detail counts. The y-axis is interpretable as percentage eﬀect of roundness because

the coeﬃcients are normalized by the baseline (precise) mean oﬀers.

For the delineation across item detail views, we indeed see lower relative discounts for

higher view rates, which bolsters H4. For the delineation across search counts, we see

a peculiar u-shape pattern where both very low and very high search counts have lower

For intuition on this, consider that quirky yet undesired items may still get a lot of traﬃc because

they are interesting.

Appendix-9

discounts than the mid range of search counts. On balance, this relationship is actually

still positive (as a linear ﬁt of these coeﬃcients has a positive slope). We surmise that

the selection eﬀect of our imperfect proxy leads to a positive bias for the thinnest market

items. Hence, we conclude only that this evidence is suggestive that thicker markets have

lower discounts (H4).

G Seller Response to Round Oﬀers

A natural extension of our analysis is to look at seller responses to round buyer oﬀers. We

limit our attention to the bargaining interactions where a seller makes at least one counter

oﬀer and compare the buyer’s initial oﬀer to level of that counter oﬀer. We derive a metric

of conciliation which indexes between 0 and 1 the distance between the buyer’s oﬀer and

the BIN (the sellers prior oﬀer). We show in Figure A-4 that round initial oﬀers by buyers

are met with less conciliatory counter oﬀers by sellers. Roundness may be used as a signal

to increase the probability of success at the expense seller revenue.

H Seller Experience

Next we ask whether or not seller experience explains this result. We might suspect that

sophisticated sellers learn to list at precise values and novices default to round-numbers.

There is some evidence for this, but any learning beneﬁt is small and evident only in the

most expert sellers. We deﬁne a seller’s experience to be the number of prior Best Oﬀer

listings prior to the current listing. With this deﬁnition, we have a measure of experience

for every listing in our data set. For tractability, we narrow the analysis to all listings with

BIN prices between $85 and $115 and focus on a single round-number, $100. Table A-8

shows ﬁrst the proportion of listings that are a round $100 broken down by the sellers

experience at time of listing. The most experience 20 percent of sellers show markedly

lower rounding rates.

By interacting our measure of seller experience with a dummy for whether the listing

is a round $100, we can identify at diﬀerent experience levels the round eﬀect on received

oﬀers. The right pane of Table A-8 shows the estimates with and without seller ﬁxed

eﬀects. Without seller ﬁxed eﬀects, we are comparing the eﬀect across experienced and

inexperienced sellers. As before, the only diﬀerential eﬀect appears in the top two deciles of

Appendix-10

experience. Interestingly, when we include seller ﬁxed eﬀects, and are therefore comparing

within sellers experiences, we see that the eﬀect is largest in the middle deciles.

Appendix-11

Table A-4: Intercepts and Slopes for Each Local Linear Regression - Through-

put

(1) (2) (3) (4) (5) (6)

Days to Oﬀer Days to Oﬀer Days to Sale Days to Oﬀer Pr(Sale) Pr(Sale)

Near round $100:

Constant 35.34

∗∗∗

40.48

∗∗∗

46.67

∗∗∗

49.62

∗∗∗

0.133

∗∗∗

0.130

∗∗∗

(0.274) (0.543) (0.355) (0.651) (0.00162) (0.00240)

Slope 0.180

∗∗∗

0.263

∗∗∗

0.641

∗∗∗

0.686

∗∗∗

0.0100

∗∗∗

0.00781

∗∗∗

(0.0582) (0.0557) (0.0742) (0.0738) (0.000735) (0.000735)

Bandwidth 6.907 7.048 7.321 7.384 2.681 2.740

N 287366 289072 224354 224389 798842 799105

Near round $200:

Constant 32.70

∗∗∗

40.05

∗∗∗

45.37

∗∗∗

50.17

∗∗∗

0.128

∗∗∗

0.115

∗∗∗

(0.482) (0.711) (0.671) (0.936) (0.00239) (0.00304)

Slope 0.442

∗∗∗

0.648

∗∗∗

0.872

∗∗∗

1.021

∗∗∗

0.00663

∗∗∗

0.00325

∗∗∗

(0.100) (0.0945) (0.137) (0.136) (0.000911) (0.000911)

Bandwidth 7.841 8.106 8.308 8.564 3.493 3.722

N 150378 150989 104398 104430 425926 426091

Near round $300:

Constant 30.37

∗∗∗

36.52

∗∗∗

42.05

∗∗∗

47.09

∗∗∗

0.120

∗∗∗

0.103

∗∗∗

(0.581) (0.627) (0.656) (0.863) (0.00285) (0.00235)

Slope -0.0746 0.0930

∗∗∗

0.144 0.204

∗∗∗

0.00562

∗∗∗

-0.00208

∗∗∗

(0.112) (0.0317) (0.0965) (0.0508) (0.000904) (0.000399)

Bandwidth 9.775 18.51 10.38 18.06 4.926 6.972

N 101507 120721 67702 75779 282623 344593

Near round $400:

Constant 26.37

∗∗∗

31.88

∗∗∗

39.25

∗∗∗

42.56

∗∗∗

0.119

∗∗∗

0.102

∗∗∗

(0.402) (0.504) (0.528) (1.019) (0.00205) (0.00245)

Slope -0.0859

∗∗

-0.0439

∗∗∗

-0.0682 -0.0131 -0.00218

∗∗∗

-0.00267

∗∗∗

(0.0425) (0.0109) (0.0429) (0.0720) (0.000428) (0.000425)

Bandwidth 16.04 29.33 20.30 17.27 6.772 6.888

N 80967 117887 51208 46905 234627 234670

Near round $500:

Constant 28.24

∗∗∗

36.29

∗∗∗

41.62

∗∗∗

47.15

∗∗∗

0.119

∗∗∗

0.0998

∗∗∗

(0.550) (0.823) (0.834) (1.209) (0.00325) (0.00364)

Slope 0.260

∗∗∗

0.314

∗∗∗

0.340

∗∗∗

0.420

∗∗∗

0.00103 -0.00113

∗

(0.0635) (0.0602) (0.0947) (0.0944) (0.000673) (0.000673)

Bandwidth 16.26 18.45 19.96 19.98 5.605 5.378

N 69122 69342 37473 37477 208351 208293

Category FE YES YES YES

Heteroskedacticity-robust standard errors in parentheses

∗

p < .1,

∗∗

p < .05,

∗∗∗

p < .01

Notes: Here we report ancillary coeﬃcients from separate local linear ﬁts according to Equation (6) in the

neighborhood of the round number indicated for the row, using the dependent variable shown for each

column, corresponding to Table 3. Heteroskedacticity-robust standard errors are in parentheses,

∗

p < .

∗∗

p < .05,

∗∗∗

p < .01.

Appendix-12

Table A-5: Oﬀers and Sales for [$99,$100) Signals

(1) (2) (3) (4)

Avg First Oﬀer $ Avg First Oﬀer $ Avg Sale $ Avg Sale $

BIN=099 -6.277

∗∗∗

-4.744

∗∗∗

-5.903

∗∗∗

-4.917

∗∗∗

(0.0974) (0.0955) (0.104) (0.106)

BIN=199 -14.21

∗∗∗

-9.742

∗∗∗

-11.75

∗∗∗

-9.035

∗∗∗

(0.333) (0.330) (0.350) (0.348)

BIN=299 -22.66

∗∗∗

-16.31

∗∗∗

-17.70

∗∗∗

-15.31

∗∗∗

(0.640) (0.398) (0.767) (0.543)

BIN=399 -32.99

∗∗∗

-22.00

∗∗∗

-22.61

∗∗∗

-17.89

∗∗∗

(0.777) (0.776) (1.116) (1.042)

BIN=499 -42.03

∗∗∗

-26.30

∗∗∗

-34.32

∗∗∗

-27.15

∗∗∗

(1.193) (1.123) (1.451) (1.302)

Category FE YES YES

Notes: Each cell in the table reports the coeﬃcient on the indicator for

BIN price

∈

[

z −

, z

) from a

separate local linear ﬁt according to equation (6) in the neighborhood of the round number indicated

for the row, using the dependent variable shown for each column. Ancillary coeﬃcients for each ﬁt are

reported in Table A-3. Heteroskedacticity-robust standard errors are in parentheses,

∗

p < .

∗∗

p < .

05,

∗∗∗

p < .01.

Table A-6: Pooling 99 and 100

(1) (2) (3) (4)

Avg First Oﬀer $ Avg First Oﬀer $ Avg Sale $ Avg Sale $

BIN=099 or 100 -4.793

∗∗∗

-3.944

∗∗∗

-4.615

∗∗∗

-4.101

∗∗∗

(0.0519) (0.0511) (0.0709) (0.0680)

BIN=199 or 200 -13.37

∗∗∗

-10.50

∗∗∗

-11.75

∗∗∗

-10.24

∗∗∗

(0.164) (0.164) (0.183) (0.183)

BIN=299 or 300 -20.90

∗∗∗

-15.30

∗∗∗

-19.04

∗∗∗

-16.52

∗∗∗

(0.352) (0.354) (0.381) (0.380)

BIN=399 or 400 -28.89

∗∗∗

-20.10

∗∗∗

-21.95

∗∗∗

-18.46

∗∗∗

(0.606) (0.611) (0.690) (0.674)

BIN=499 or 500 -40.48

∗∗∗

-26.66

∗∗∗

-34.77

∗∗∗

-28.58

∗∗∗

(0.923) (0.924) (1.083) (1.083)

Category FE YES YES

Notes: Each cell in the table reports the coeﬃcient on the indicator for

BIN price

∈

[

z −

, z

] from a

separate local linear ﬁt according to a modiﬁed version of equation (6) in the neighborhood of the round

number indicated for the row, using the dependent variable shown for each column. Ancillary coeﬃcients

for each ﬁt are reported in Table A-3. Heteroskedacticity-robust standard errors are in parentheses,

∗

p < .1,

∗∗

p < .05,

∗∗∗

p < .01.

Appendix-13

Table A-7: Round Numbers and the Buy-it-Now Option

(1) (2) (3) (4)

Pr(BIN) Pr(BIN) Pr(BIN|Sale) Pr(BIN|Sale)

BIN=100 0.00595

∗∗∗

0.00757

∗∗∗

-0.0194

∗∗∗

-0.0172

∗∗∗

(0.00103) (0.000893) (0.00278) (0.00286)

BIN=200 0.00556

∗∗∗

0.00611

∗∗∗

-0.0154

∗∗

-0.0156

∗∗

(0.00138) (0.00137) (0.00770) (0.00768)

BIN=300 0.000860 0.000959 -0.0281

∗∗

-0.0228

∗∗∗

(0.00176) (0.00111) (0.0117) (0.00705)

BIN=400 0.00395

∗∗∗

0.00397

∗∗∗

0.000880 -0.00766

(0.00121) (0.00118) (0.00831) (0.00826)

BIN=500 0.00315

∗∗∗

0.00463

∗∗∗

-0.000596 -0.00358

(0.00100) (0.00119) (0.0112) (0.0102)

Category FE YES YES

Notes: Each cell in the table reports the coeﬃcient on the indicator for roundness from a separate local

linear ﬁt according to equation (6) in the neighborhood of the round number indicated for the row, using

the dependent variable shown for each column. Ancillary coeﬃcients for each ﬁt are reported in Table

A-3. Heteroskedacticity-robust standard errors are in parentheses,

∗

p < .1,

∗∗

p < .05,

∗∗∗

p < .01.

Appendix-14

Figure A-3: H4

−.14 −.12 −.1 −.08 −.06

0 2 4 6 8 10

View Item: Round $100

−.12 −.1 −.08 −.06 −.04

0 2 4 6 8 10

SRP: Round $100

−.18−.16 −.14−.12 −.1 −.08

0 2 4 6 8 10

View Item: Round $200

−.15 −.1 −.05

0 2 4 6 8 10

SRP: Round $200

−.18−.16−.14−.12 −.1 −.08

0 2 4 6 8 10

View Item: Round $300

−.15 −.1 −.05

0 2 4 6 8 10

SRP: Round $300

−.2 −.15 −.1 −.05

0 2 4 6 8 10

View Item: Round $400

−.15 −.1 −.05

0 2 4 6 8 10

SRP: Round $400

−.25 −.2 −.15 −.1

0 2 4 6 8 10

View Item: Round $500

−.2 −.15 −.1 −.05

0 2 4 6 8 10

SRP: Round $500

Notes: This ﬁgure plots the point estimates and conﬁdence interval of the local linear estimation of the

round number BIN eﬀect on mean ﬁrst oﬀers for each decile of view item detail counts and search result

exposure counts.

Appendix-15

Figure A-4: Seller Response to Buyer Oﬀers

.36 .38 .4 .42 .44

Avg Cave Rate [(BIN−Cntr)/(BIN−Offr)]

0 200 400 600

Offer

Round $50 Other $ Increment

Notes: This scatterplot presents average seller counteroﬀers, normalized by the listing price price to be

between zero and one, grouped by unit intervals of the buyer oﬀer. When the buyer oﬀer is round to the

ﬁfties, the average seller oﬀer is represented by a ﬁlled red circle.

Appendix-16

Table A-8: Seller Experience and Round Numbers

Percent Round $100 Percent 99

1st Decile 0.164 0.0904

(0.00224) (0.00174)

2nd Decile 0.139 0.0982

(0.00201) (0.00172)

3rd Decile 0.127 0.0981

(0.00197) (0.00176)

4th Decile 0.118 0.105

(0.00182) (0.00174)

5th Decile 0.107 0.108

(0.00165) (0.00164)

6th Decile 0.102 0.118

(0.00155) (0.00163)

7th Decile 0.0927 0.122

(0.00142) (0.00159)

8th Decile 0.0822 0.124

(0.00129) (0.00151)

9th Decile 0.0683 0.129

(0.00113) (0.00146)

10th Decile 0.0507 0.126

(0.000914) (0.00131)

N 234635 234635

Avg First Oﬀer Avg First Oﬀer

Round $100 x 1st Decile -8.257

∗∗∗

-1.386

(0.700) (2.168)

Round $100 x 2nd Decile -8.377

∗∗∗

-3.314

∗∗∗

(0.633) (1.053)

Round $100 x 3rd Decile -7.502

∗∗∗

-2.157

∗∗

(0.614) (0.848)

Round $100 x 4th Decile -7.761

∗∗∗

-2.653

∗∗∗

(0.560) (0.705)

Round $100 x 5th Decile -7.988

∗∗∗

-2.544

∗∗∗

(0.513) (0.607)

Round $100 x 6th Decile -9.299

∗∗∗

-3.260

∗∗∗

(0.461) (0.519)

Round $100 x 7th Decile -9.358

∗∗∗

-3.518

∗∗∗

(0.422) (0.455)

Round $100 x 8th Decile -9.489

∗∗∗

-3.910

∗∗∗

(0.373) (0.391)

Round $100 x 9th Decile -9.925

∗∗∗

-3.889

∗∗∗

(0.326) (0.333)

Round $100 x 10th Decile -11.84

∗∗∗

-5.414

∗∗∗

(0.250) (0.248)

Category FE YES

Seller FE YES

Notes: The left table documents prevalence of round-number listings by deciles of seller experience, where

seller experience is measured by the number of past transactions. Standard deviations are presented in

parenthesis. The right table replicates estimates of

00 separately by decile of seller experience. Standard

errors are in parenthesis.

Appendix-17